| Day |
Date |
Activity |
Assignment (due one week from assignment date, unless otherwise stated) |
| Tue | 1/10 |
Welcome/Fun and Games |
Read Probability (Idea #33 in the text -- pp. 124-127), and
the birthday problem (Idea #33 in the text -- pp. 132-135) for next time,
Thursday, 1/12. You might also check out my on-line
explanation of the birthday problem, for comparison. Consider playing "Let's Make a Deal"
(so that you better understand it -- here's a good
description of the game). Both of these problems are examples of
Probability problems.
|
| Thu | 1/12 |
Fun and Games |
For next time:
- Read Idea 01, Zero, pp. 4-7
- Read Idea 09, Primes, pp. 36-39
Homework 1 (due Thu, 1/19):
Put your name at the top of the paper and label it Math 115 - Homework 1. For each problem show me how you found the answer - unsupported answers are worth nothing. Feel free to explain your reasoning and, if you wish, you may include any incorrect attempts at the problem. If you use an outside source you should reference that source!
-
Carefully write out a solution to the problem about the genie, the gem,
and the three scales. Since we have discussed this in class already this will
be graded on how well you write up your answer. Be sure to explain the solution
carefully and include all the possibilities. Feel free to draw diagrams if you
wish.
- There are 5 people trapped in an elevator. Being really bored one of them
bets the others that at least two of them were born on the same month of the
year. What is the probability she wins this bet? ( You may assume that it is
equally likely to be born on any given month. this may not be strictly true,
but it is close enough that the final probability wouldn't change very
much.)
- Flip a fair penny and a fair dime. What is the likelihood that
a. both come up heads
b. they come up with different results?
Hint: If you find this difficult, you might want to list out the universe of all possible flips.
- Roll two standard (fair) dice. What is the probability you roll
a. a two?
b. a seven?
c. a 14?
|
| Tue | 1/17 |
Zero and Natural Numbers |
For next time:
- Read Idea 03, Fractions, pp. 12-15
Homework 2: similar instructions as last time (due Tuesday, 1/24):
- Suppose that you're at the grand opening of a grocery store, and you and
Bob (another "contestant") each choose a jar of peanut butter, at random, from
a display of 10 different jars of peanut butter. Under one jar is the key to a
NEW CAR! Under the others is a picture of a donkey. The owner of the store
shows that under seven of the (unchosen) jars there are pictures of
donkeys. You're offered the chance to switch for one of the other two jars --
Bob's jar, or the jar not taken but still unturned. Do you switch, and, if so,
for which one -- Bob's or the unchoosen jar? You must carefully explain your
reasoning, and give the probabilities of winning depending on the three
possible choices. You might consider simulating the game and show data that
supports your decision.
- Write the prime factorizations for
- 1008
- 1009
- 1010
|
| Thu | 1/19 |
Prime and Rational Numbers |
For next time:
- Please read the brief description on primitive
counting (remembering that I've modified the technique a little -- to count
down to 1, instead of to two or three).
- Read Idea 02, Number Systems, pp. 8-11
Homework 3 (due Thursday, 1/26):
- Find two distinctly different ways to write each of the following fractions as a
sum of three different fractions:
- 1/2
- 2/3
- Use the rules of fractions to illustrate (as indicated in our text) that

- Solve the following shopping problems involving fractions:
- An item originally costing $100 is marked down 20%; then marked
down an additional 30%. What is the cost of the item? How much is it
marked down from its original price?
- An item now costs $22. It was marked down twice: 30% the first
time, and then 50% on top of that. What was its original price?
- Illustrate the following statements about prime numbers by showing
two specific examples of each:
- Goldbach conjecture - Every even number (greater than two) is the
sum of exactly two prime numbers. For example 18=11+7
- Primes of the form 4k+1 can be written a the sum of
two squares in exactly one way: so for k=3,

|
| Tue | 1/24 |
Primitive Counting |
|
| Thu | 1/26 |
Egyptian Math |
Homework 4 (due Thursday, 2/2):
Solve the following problems
- Write the prime factorizations for
- 3451
- 5223
- Use the method of "counting by partition" to count the following (show the entire tree, and the string of ones and zeros that results):
- Use the method of "counting by partition" backwards to report the number of sheep corresponding to the following strings:
- 1, 0, 0, 1, 0, 1, 0
- 1, 1, 0, 1, 0, 1
- 1, 1
- 1, 0, 1, 1, 0
- In the binary card trick (Fraudini's trick -- see this on-line description),
- What number (from 1 to 63) is one thinking of if the only cards chosen are
- the card with all the odds from 1 to 63, and
- the card with all the numbers from 32 to 63?
- If I'm thinking of the number 42, describe which cards I'll choose.
|
| Tue | 1/31 |
Egyptian Math |
|
| Thu | 2/2 |
Egyptian Division |
For next time, read this on-line
introduction to bases.
Homework 5 (due 2/9):
- Demonstrate Egyptian multiplication by multiplying:
- Demonstrate Egyptian division by dividing:
Try these using the same sort of "doubling/halving" table that
we use for multiplication.
- Demonstrate Egyptian division by dividing:
Try these using the unit fractions table method, and Fraudini's
trick (writing a number as a sum of distinct powers of 2).
|
| Tue | 2/7 |
Bases |
Homework (due Tue 2/14):
- Rewrite the number we know as 2977 (written in base 10), only using
- base 2
- base 8
- base 16
- base 5
- Rewrite the following numbers in base 10:
- 101001010012
- 735568
- DB92F16
- Show how to add 2268 and 3758 (both numbers
expressed in base 8).
|
| Thu | 2/9 |
Bases/Babylonian/Mayan Math |
Homework (due Tuesday, 2/21):
- How would the Mayans write
- How would the Babylonians write
- Here's another mystery for you:
Explain how Lewis Carroll was using unusual bases to do the strange math in
chapter two of Alice
in Wonderland? On about the third page of chapter
two (after the graphic of "Giant Alice watching Rabbit
run away"), Alice starts speaking out some bizarre
equations:
"Let me see: four times five is twelve, and four times
six is thirteen, and four times seven is -- oh dear! I
shall never get to twenty at that rate!"
Find some reasonable bases to make the "calculations"
work out....
|
| Tue | 2/14 |
Fibonacci Numbers |
|
| Thu | 2/16 |
Exam I |
|
| Tue | 2/21 |
Fibonacci Numbers |
Read the section on Fibonacci numbers (Idea #11, p. 44).
Read more about Fibonacci Nim.
|
| Thu | 2/23 |
Fibonacci Spirals |
For next time: please read Golden Rectangles (Idea #12, p. 48).
Homework (due Thursday, 3/1):
- I want you to visit this website and turn your own image into a Fibonacci spiral. Choose an appropriate image, then create and then email me a copy of your own spiral image. Make one that everyone will enjoy, as I will create a gallery of images.
Make sure that you send me the final image, and not just a link
(that won't do anything!). Right click on the image, and save it to
your computer -- then past the image into your email. That's the
easiest way, I think.
- Fibonacci Nim:
- Suppose you are about to begin a game of Fibonacci
nim. You start with 50 sticks. What's your first move?
- Suppose you are about to begin a game of Fibonacci
nim. You start with 100 sticks. What's your first move?
- Suppose you are about to begin a game of Fibonacci
nim. You start with 500 sticks. What's your first move?
- Suppose you begin a game of 15 sticks by taking 2; your
friend takes 4; what's your next move, that will lead to
victory provided you know the strategy?
- By experimenting with numerous examples in search of a pattern,
determine a simple formula for
^2+(F_{n})^2})
that is, a formula for the sum of the squares of two consecutive
Fibonacci numbers. Try various values of n (at least five
different values) to see what happens.
- By experimenting with numerous examples in search of a pattern,
determine a simple formula for
^2-(F_{n-1})^2})
that is, a formula for the difference of the squares of two
non-consecutive Fibonacci numbers.
- The rabbits rest. Suppose we have a pair of baby rabbits
-- one male and one female. As before, a pair cannot reproduce
until they are one month old. Once they start reproducing,
they produce a pair of bunnies (one bunny of each sex) each
month. This new pair will do the same as the parent pair --
mature, and reproduce following the same rules. Now, however,
let us assume that each pair dies after three months,
immediately after giving birth. Create a chart showing how
many pairs we have after each month from the start through
month seven.
|
| Tue | 2/28 |
Golden Rectangles |
|
| Thu | 3/1 |
Golden Rectangles |
Reading assignments (for 3/13, following break):
Homework (due Thursday, 3/15):
- Create the next row in both Pascal's triangle and in the Chinese versions (see day 16
- Find seven examples of rectangles in your daily life. Measure the side lengths, and compute the ratio of the larger to the smaller dimension. Are any of them golden?
|
| Tue | 3/6 |
Spring Break |
|
| Thu | 3/8 |
Spring Break |
|
| Tue | 3/13 |
Platonic Solids |
|
| Thu | 3/15 |
Platonic Solids |
|
| Tue | 3/20 |
Graphs |
You have a new homework assignment:
- Part of it is a reading assignment: for next time, please read about Graphs, Idea 29, p. 116.
- You also have some problems related to Platonic solids (due next Tuesday, 3/27):
- Explain how this image (of Earth...) is related to Platonic solids.
- In your own words, explain why no Platonic solid has
- hexagonal faces
- octagonal faces
- Find an example of a company's logo which involves Platonic solids (don't use those you find using these resources, but they'll get you started):
- Logos!
-
 (explain how this one is related to Platonic solids) (explain how this one is related to Platonic solids)
- Draw 2-dimensional projections of each of the Platonic
solids. That is, a realistic view of a platonic solid on 2-dimensional
paper. Try your hardest to do this well!
- For each of the Platonic solids, compute the following:
 where F is the number of faces, E the number of edges, and
V the number of vertices. What do you discover?
where F is the number of faces, E the number of edges, and
V the number of vertices. What do you discover?
- Find a soccer ball and try the same thing (
 ) on that: what do you discover? ) on that: what do you discover?
|
| Thu | 3/22 |
Graphs |
Homework (for Thursday, 3/29):
- Here is another situation that Euler considered:
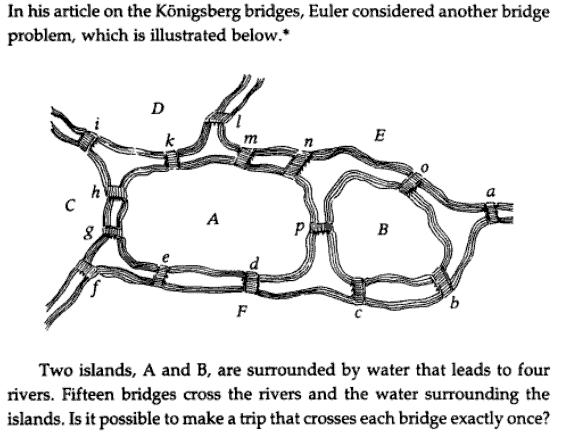 Is the new, improved Konigsberg walk possible? Draw the corresponding graph and
explain!
Is the new, improved Konigsberg walk possible? Draw the corresponding graph and
explain!
- Draw your family tree (as a directed graph) with one of your grandparents as the root of the
tree (include only those actually descended from that
grandparent). Label each vertex (that is, each person!).
|
| Tue | 3/27 |
Links |
Homework (for Thursday, 4/5):
- I found this interesting worksheet
on the web. Complete the worksheet. On the first page ("Problem 0"),
decide whether each graph has an Euler path or not. For the other three
pages, follow the instructions.
|
| Thu | 3/29 |
Knots |
You have a new reading assignment for next time: visit
this website and read about "human knots": have you ever played this before? |
| Tue | 4/3 |
Exam II |
|
| Thu | 4/5 |
Knots |
|
| Tue | 4/10 |
Mobius Bands |
Homework, due Tuesday, 4/17:
- Identify the knots (or links?) in this "story", which I call A
Knotty Tale. You may need to apply the Reidemeister moves to
convince yourself that a picture of a knot is really the unknot, say,
but you don't need to tell me how you determined which knot or link
each one is. Just put a name next to each one.
|
| Thu | 4/12 |
Mobius Bands |
You have a new reading assignment:
|
| Tue | 4/17 |
Fractals |
Please read Idea #25, Fractals (p. 100) for next time.
Homework (due Tuesday, 4/24):
- Twist a band in two different ways:
- four times, and
- five times,
and cut the band down the middle. What objects result? Describe them exactly,
specifying their number of half twists, how they're connected, etc.
- Describe exactly what you get if you cut a thrice-twisted band in thirds
(as we did in class to the Mobius band).
- Relate the following logo to twisted bands (e.g. Mobius bands):

- Is the following recycling symbol correct (i.e. Mobius) or not?

- Find two examples of the recycling symbol on nationally known products,
one Mobius and the other not Mobius. Name the products, and draw (or print) the symbols.
For the Mobius band cutting, you will want to use long and wide bands -- it makes seeing what's going on much easier.
|
| Thu | 4/19 |
Fractals |
Due 4/24: Try my funhouse mirror generator: make your own
funhouse mirror image, using my web
interface and your own image, and I'll post them on our "website gallery".
|
| Tue | 4/24 |
Infinity |
|
| Thu | 4/26 |
Logo Day |
|
| Tue | 5/1 |
Final |
1:00-3:00 p.m. |
 (explain how this one is related to Platonic solids)
(explain how this one is related to Platonic solids)

