Day 15, MAT115

• #1: you need the zero on 360, and the Mayans had one!
• #2: you need the zero on 360, but the Babylonians didn't have one:(.
• Lewis Carroll was always messing with people's heads. Let's take a look at what we THINK he (or rather Alice) was up to....

  "Let me see: four times five is twelve, and four times six is thirteen, and four times seven is -- oh dear! I shall never get to twenty at that rate!"

In fact, it appears that successive Fibonacci numbers are important.

1. The side lengths were in successive Fibonacci numbers; and
2. the ratio of the side lengths of the rectangles were settling down to a number in the vicinity of 1.6.

As we move toward the concepts of the so-called "golden mean" and "golden rectangle", we start with a nice Fibonacci spiral (e.g. this site).

The process of creating a Fibonacci spiral is simple:

• Start: Draw a square (a special rectangle).
• To each rectangle, attach the largest square possible to make a new rectangle. Make sure that you always proceed in the same direction (clockwise, or counter-clockwise).
• Do it again, do it again, do it again....

Make sure that you send me the final image, and not just a link (that won't do anything!). Right click on the image, and save it to your computer -- then past the image into your email. That's the easiest way, I think.

Demi, Meghan, and Krystal have started us off....

• "The Sexiest Rectangle" - or is it just cute?
  • Important property: if you cut out the largest square possible, you still have a golden rectangle! There's a "world within a world" in the golden rectangle....

  • The golden mean (or golden ratio, golden section) -- A "precious jewel" (Johannes Kepler)
    • derived by ratios of Fibonacci numbers, or
    • using the rectangle directly. The Greeks defined a golden rectangle by calling it the rectangle which, when the largest square possible is removed, retains its shape (which means that the ratio of side lengths doesn't change).
    • The golden rectangle has side lengths in the ratio

      Note that the value is only approximately 1.618: is an irrational number, like , and its decimal representation goes on forever and never repeats:

      

  • What sizes do U.S. flags come in?

  • How might you use the golden rectangle to make life more interesting?

• The Golden Rectangle in Art and Architecture

  or not? Many people think that if you look hard enough, you'll find them - or any rectangles you're particularly interested in!

  • Architecture: The Parthenon
  • Art: St. Jerome

• Where might you find a golden rectangle? (Hint: what's in your wallet?)

• Now: what kind of rectangle will you get if you repeat the Fibonacci spiral process with another kind of rectangle to start (rather than a square)?

  Turns out, that if you do it over and over and over again, you'll get a rectangle that gets more and more golden.

  Let's try: we'll use a piece of grid paper (looking short and squat), and a 3x1 rectangle (start it running the tall-way at the 12th row down, 8th cell over).

  Now, let's figure out what the recurrence relation is for the dimensions of our rectangles, and then figure out if we're getting golden....

• The A0 Paper Fractal

  "A paper" is something you've no doubt encountered before: it's the long sheets we occasionly use (usually "A4" paper), which is far more common in Europe.

  "A paper" is constructed so that, if folded in half (do we say the long way or the short way?), you get a sheet which has exactly the same shape -- that is, the ratio of its side lengths is the same as the original sheet.

  

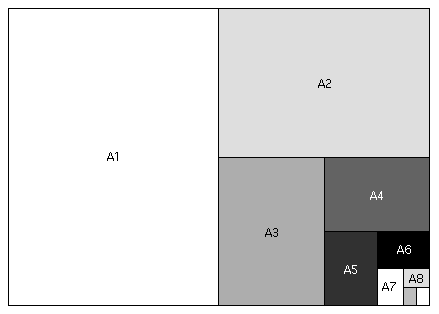
  Let's see what the dimensions of A paper must be so that this requirement is fulfilled....

  Call the long dimension of the A1 paper above , and the short dimension 1.

  • Then what are the dimensions of the A2 paper, according to the design of A paper?
  • What is the value of ?

• Why not an A0 paper spiral? Let's try that.... This is the spiral, created using non-squares each time:
  

  In both cases there's "the world within the world". Both are fractals.