- Announcements:
- Your homeworks are graded:
- Your Fibonacci spiral is graded separately, and is worth a
homework. Basically it's a binary world -- you did it or you
didn't. But I'll give a few prizes to the best of the lot.
- The Fibonacci homework
- Problems 3 and 4:
- I warned about "index migration" -- and
then it happened!
- Yes the sums or squares or differences are
Fibonacci numbers -- but tell me more!
- There was ambiguity in the rabbit problem. I'll
show you what I had in mind, and how it was solved.
- The Pascal homework
- The withdrawal date is coming up. If you'd like to talk to me
about your progress before that date, please make an appointment to see
me or stop by during my office hours.
- You have a new homework assignment (due next Tuesday).
- Part of it is a reading assignment: for next time, please read about Graphs, Idea 29, p. 116.
- You also have some problems related to Platonic solids.
- Question of the Day:
How are Platonic solids related to graphs?
- Today we begin talking about graphs.
- Graphs:
- The Bridges
of Konigsberg problem: "is it possible to set off and walk around Konigsberg crossing each bridge exactly one?" (p. 116)
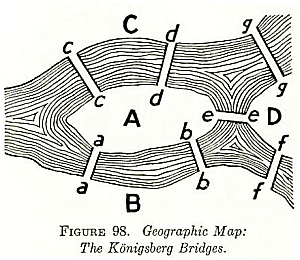

- Solved by Euler
(1735), the beginning of graph theory.
- Graphs are made up of vertices (points) and edges
that connect the vertices. More formally, a graph is
- A collection of points, called vertices.
- A collection of edges, each of
which connects two vertices.
- The degree of a vertex is the number of edges
coming into it.
- Euler's solution:
- Konigsberg: To be traversable, there must be at
most two vertices of odd degree.
- Euler noticed the hand-shaking theorem: in any
graph, the number of vertices with odd degree
must be even.
- An alternative
solution -- thanks to spiked math
- Which of the Platonic solid graphs can be traversed
without backtracking? (here
they are)
- You've
probably been making graphs for a long time.... (the pentagram)
- Definition of a graph: a graph is
- a collection of vertices,
- a collection of edges, and
- a set of rules, one for each edge, telling how each edge is
connected to its pair of vertices.
- Graphs don't change by bending edges, but breaking them or
detaching edges from their vertices (and hence creating new vertices)
gives new graphs.
- A graph is simple if it doesn't have any loops (edges connected
from a vertix to itself), or multiple edges with the same two vertices.
- Exercise: draw all the simple graphs with three vertices.
- A cycle is a route from a node back to itself that
doesn't retrace steps.
- One of these graphs is a tree: a graph that has no cycles.
- Where have we seen trees used before?
- Duality -- again!
- Exercise: you draw all the simple graphs with four vertices.
- Have you ever seen any of these before? Could we give any
of them names?
- Planar graphs are graphs that can be drawn such that no two edges
intersect. Every Platonic
graph can be drawn this way, so they are planar graphs.
- Complete graphs are simply graphs with connections between
every pair of vertices (but no loops).
- Exercise: Let's see if we can show that the complete graph
with five vertices is not planar:
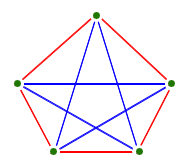
- We can show that the complete graph with four vertices is
planar.
- Why not? What happens?
- The three utilities and three houses graph is not planar:

- Any non-planar graph has a copy of one of these two graphs
in it somewhere, as a subgraph:

Links:
Website maintained by Andy Long.
Comments appreciated.




