Today:
- Announcements:
- Assignment returned:
- #4, p. 418 -- simplify!
- #38 -- the equation of a tangent line is of the form
-- an affine function.
- #66:
- You were to study this function, which means find domain, intercepts, asymptotes, regions of increase and decrease, inflection, symmetry, etc.
- There is symmetry -- but the function is neither odd nor even. Since the "inside function" is symmetric (about
), so is the composition itself:
- Your quiz opportunity today is over section 7.1.
- Your lab assignment (DEs) is due today.
- We need to wrap up yesterday's topic: L'Hopital's Rule
- Motivation of L'Hopital's Rule (requires the limit definition
of the derivative -- p. 471)
- Examples:
- #29, p. 477
- #70, p. 478
- #86, p. 478
- #93, p. 479
- Today we begin Section 7.1: Integration by parts.
- We'll motivate this topic by considering exercise #66, p. 494 in detail.
- Derivation of the integration by parts formula:
v'(x)dx=u(x)v(x)-\int_{}^{}v(x)u'(x)dx})
- First of all, the big picture: integration by parts is just the
product rule backwards. This integration technique, like all
integration techniques, is really just a differentiation technique in
reverse.
- Integration by parts may need to be carried out multiple times:
sometimes the idea is to simplify the integral each time, until a
really simple one arises allowing us to calculate the final solution
(e.g. Example 6, p. 491). Sometimes it's something of a trick: we
compute the integral multiple times in order to return to the original
integral, allowing us to solve an equation for the original integral
(e.g. Example 4, p. 490).
- Suggested strategy:
- Choose u so that u' is simpler than u
itself.
- Choose v' so that
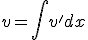can be evaluated.
- Sometimes v'=1 is a good choice.
- Of course, all this works with definite integrals:
- Examples:
- #9, p. 492
- #10
- #26
- #39
- #40
- #51
Website maintained by Andy Long.
Comments appreciated.