Day 33 in MAT229

Today:

• Announcements:

  • Your homework for 11.3 is due.

• Section 11.4: Comparison Tests

  • Theorems:

    

    Notice how we can use each series to inform us about the other:
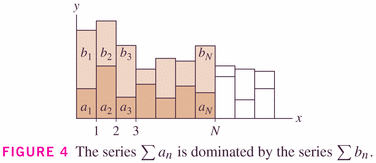
    1. if the series of the if finite, so is the smaller series of ;
    2. if the series of the if infinite, so is the larger series of .

    

    This comparison means that we'll need some series in our tool box with which to compare other series. The two obvious candidates are
    1. geometric series, and
    2. p series, including
    3. the harmonic series (to show divergence).
    But once we have a known series, we can throw it into our toolbox, too!

    

    This theorem says that, in the long run, one series has terms which are simply a constant times the terms in the other series.

    In "the long run" means that we only really need to worry about the "tails" of series: we can throw away any finite number of terms for issues of convergence.

  • Examples:
    • #6, p. 750
    • #16
    • #28
    • #34 (draw a picture)
    • #46

• Section 11.5: Alternating Series
  Once again, our mission here is not necessarily the value of the series, but may be simply knowledge of whether it converges or not.

  That being said, Theorem 2 below does give us some help in determining the value of (or at least bounds on the value of) the series of a type called an "alternating" series.

  

  How do they reach the conclusion that the sum is positive and at most ?
  
  • Examples:
    • The alternating harmonic series is convergent (Example 1, p. 753).
    • #5, p. 755
    • #13
    • #17
    • #23
    • #27
    • #34

• Section 11.6: Absolute versus Conditional Convergence, and ratio and root tests
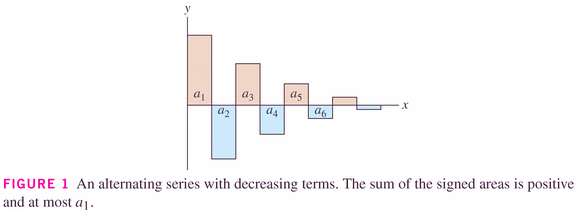
  • First, a definition:

    

    Let's think of a couple of examples of
    • Series that converge absolutely, and
    • Series that don't.

    

    

  • Examples:
    • #5, p. 761
    • #12, p. 761

    • It turns out that conditionally convergent series can have their terms rearranged to converge to any limit you like (see "Rearrangements", on p. 761). Hmmm.... Is this the end of commutativity?!

  • The Ratio and Root Tests
    • There are two main tests for convergence of series in this section:

      

      This result says that eventually the ratio of successive terms is effectively constant, : what kind of series looks like that? A geometric series:

      

      Examples:
      • #2, p. 761
      • #3, p. 761

      

      This result says that eventually the absolute values of the terms are effectively equal to : what kind of series looks like that? A geometric series!

      No wonder the results of the tests look exactly the same.... Too bad Rogawski didn't just use the same letter for the limits in both cases!

      

      Notice that, once again, limits of sequences plays an important role! Series are just sums of sequences, after all; we're focused on how terms behave (root test), how successive terms behave (ratio test), or how partial sums behave.

      Examples:

      • #7, p. 761
      • #13, p. 761