Day 42 in MAT229

Today:

• Announcements:

  • You have a homework due tomorrow.
  • Quiz opportunity tomorrow is over 11.10.
  • Homework returned:
    • 4, p. 765 -- convergent by AST; only conditionally convergent.
    • 8 -- Divergent by ratio test
    • 20 -- convergent by comparison with

  • Quiz returned:

• Section 11.9: Representations of Functions as Power Series
  • Summary:

    As described in class, once we have one power series, we have an infinite number of other power series. We can use function composition to create others. So, for example, from , we can produce series for

    1. 
    2. 
    3. 

    The other very important notion discussed here is the validity of differentiation and integration of power series. And the big news is that both operations are legitimate on the interval of convergence of the original power series. Hence, we can also generate the following power series from the series for :

    1. What do you get when you integrate ? How can we find a power series for this function?
    2. Given the power series for : what would be the power series of its anti-derivative(s)?

  • Examples:
    • What do we get when we differentiate the series for term-by-term?
    • Worksheet we are using today
    • #5, p. 775
    • #9
    • #29

• Section 11.10: Taylor and MacLaurin Polynomials
  • The big picture: we're approximating functions (some nasty) with nice ones (polynomials):

    

    

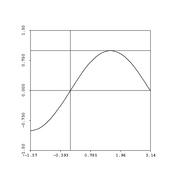
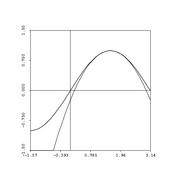
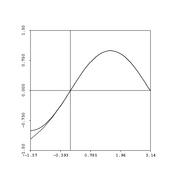
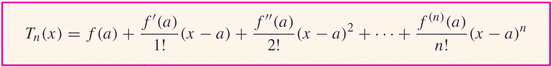
    Let's talk error now. Remember error? As we discussed for the case of Simpson's rule, it's nice to give an estimate -- but even nicer when you can provide an error estimate, also....

    
    
    

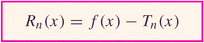
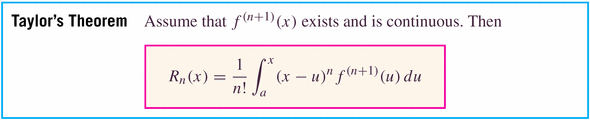
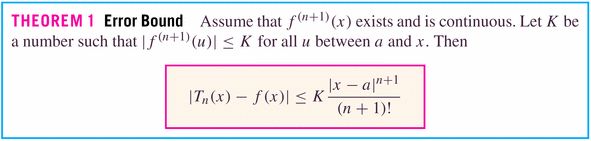
  • Examples:
    • Taylor Polynomials Lab (from Stewart's Calculus)

• Worksheet we are using today
• Worksheets from the University of Arizona