Day 51 in MAT229

Last time

Next time

Today:

Announcements:
- Return of your homework:
  - 10
  - 14
  - 36
- You have a homework due today, over 12.2.
- Quiz Opportunity over section 12.4
- You do have an exam next Thursday: it will cover everything up through 12.3 since our last exam.
Section 12.3: The Dot Product
- An example problem, in which we need a "shadow casting" function: Eratosthenes and the calculation of the radius of the Earth.
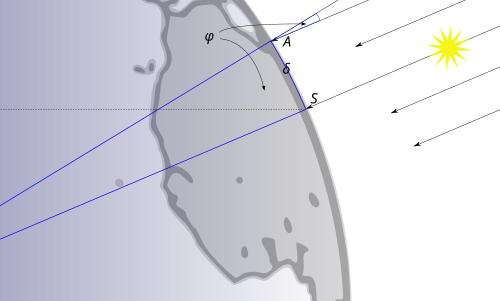
- Now let's think a little more about how we resolve the vector forces into components: we'll find it convenient to define a product of two vectors as follows:
  
  (how would you define this for vectors in two-space?). It's just component-wise multiplication, and we add up the results.
  examples:
  - #1, p. 830
  - #5
  - #11
  It turns out that
  
  where
  
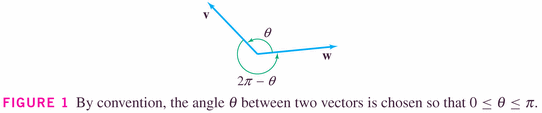
  Otherwise, the angle is acute.
  
  examples:
  - #15, p. 830
  - #17
  Finally then, we can put it all together to get this:
  
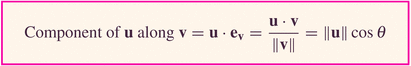
  In a way, this is the "shadow" of vector u along v's direction (notice that v's length has been accounted for, by using the unit vector in the v-direction).
- Additional examples:
  - #49, p. 831
  - #51
  - #57
Section 12.4: The Cross Product
- The next product we'll find convenient to define is the cross product, which is a product of two vectors resulting in a third vector, which juts into the space perpendicular to which the two vectors live.
  It is only defined (and useful) in three-space, which makes it somewhat unusual (the dot product exists and is useful in any dimensional space).
  The cross product is linear in its components: that is,
  
  ${(\bf{v}_1+\bf{v}_2)\times(\bf{w}_1+\bf{w}_2)}=\bf{v}_1\times\bf{w}_1+\bf{v}_1\times\bf{w}_2+\bf{v}_2\times\bf{w}_1+\bf{v}_2\times\bf{w}_2$
  This means that we can define it on the unit vectors in three space, and then deduce it using the component-wise definition of a three-vector.
  
  ${\hat{i}\times\hat{j}=\hat{k}}$
  ${\hat{j}\times\hat{k}=\hat{i}}$
  ${\hat{k}\times\hat{i}=\hat{j}}$
  
  When you reverse direction, however, you get the negative of the clockwise results:
  
  ${\hat{i}\times\hat{k}=-\hat{j}}$
  ${\hat{j}\times\hat{i}=-\hat{k}}$
  ${\hat{k}\times\hat{j}=-\hat{i}}$
  
  Furthermore, if you cross a vector with itself you get the zero vector:
  
  ${\hat{i}\times\hat{i}=\hat{j}\times\hat{j}=\hat{k}\times\hat{k}=\bf{0}}$ Example:
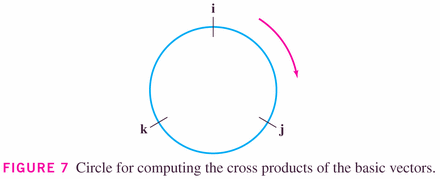
  - #5, p. 838
  Now: here are the important geometric (rather than simply algebraic) properties of this product:
  
  Notice the difference in length between the dot- and cross-products:
  for the dot-product, it's the cosine; for the cross-product, it's the sine.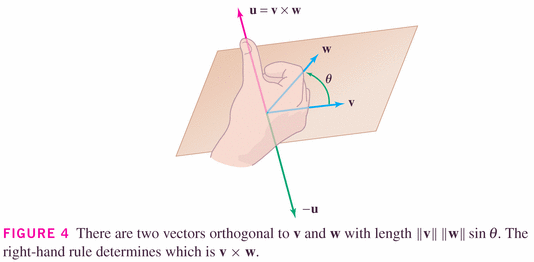
  
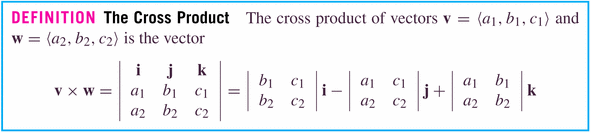
  There's another way of calculating the cross-product, which helps organize the calculation, and you may find it useful:
  
  So let me explain what's going on....
  The "absolute values" in this case represent determinants, which, for a 2x2 system with first row a, b and second row c, d is given by ${ad-bc}$ . So the computation above works out to
  
  ${\bf{v}\times\bf{w}=\bf{i}(b_1c_2-c_1b_2)-\bf{j}(a_1c_2-c_1a_2)+\bf{k}(a_1b_2-b_1a_2)}$
  Example:
  - #7, p. 838
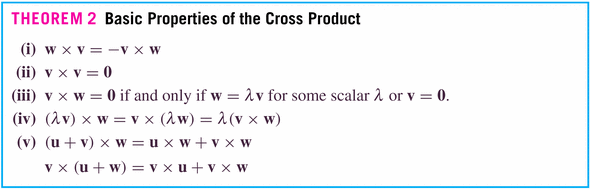
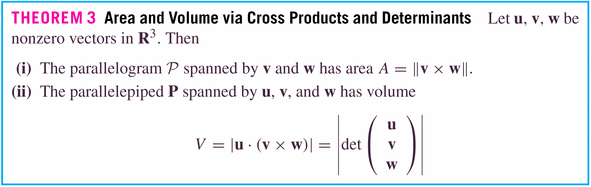
  Examples:
  - #15, p. 838
  - #33, p. 839
  - Torque: #39
  - Torque: #41
  - A cross-product (and dot product) worksheet
Links
- Some nice calculus worksheets

Website maintained by Andy Long. Comments appreciated.