Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
If 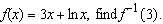 Select the correct answer.
|
|
|
2.
|
Evaluate the integral. 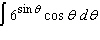 Select the correct
answer.
|
|
|
3.
|
If 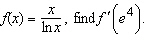 Select the correct answer.
|
|
|
4.
|
Differentiate the function. 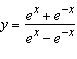 Select the correct
answer.
|
|
|
5.
|
Find the average value of the function on the given interval. 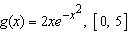 Select the correct answer.
|
|
|
6.
|
Differentiate the function. 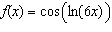 Select the correct
answer.
|
|
|
7.
|
Find the derivative of the function. 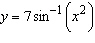 Select the
correct answer.
|
|
|
8.
|
Find the volume of the solid obtained by rotating the region bounded by the
given curves about the specified line. 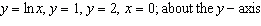 Select the correct
answer.
|
|
|
9.
|
Use logarithmic differentiation to find the derivative of the function.
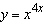 Select the correct answer.
|
|
|
10.
|
Find the limit. 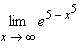 Select the correct
answer.
|
|
|
11.
|
Evaluate the integral. 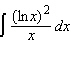 Select the correct
answer.
|
|
|
12.
|
Find the volume of the solid obtained by rotating about the y axis the
region bounded by the curves. 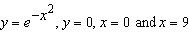 Select the
correct answer.
|
|
|
13.
|
Calculate g(x), where 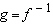 . State the domain and range of
g. Calculate 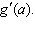 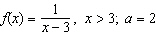 Select the correct
answer.
|
|
|
14.
|
Express the quantity as a single logarithm. 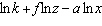 Select the
correct answer.
|
|
|
15.
|
Use the properties of logarithms to expand the quantity. 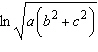 Select the correct answer.
|
|
|
16.
|
Differentiate the function. 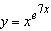 Select the correct
answer.
|
|
|
17.
|
Find the limit. 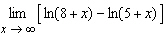 Select the correct
answer.
|
|
|
18.
|
At what point of the curve 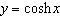 does the tangent line have slope
4? Select the correct answer.
|
|
|
19.
|
Find an equation of the tangent line to the curve 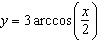 at the point 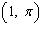 . Select the correct answer.
|
|
|
20.
|
Evaluate the integral. 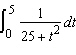 Select the correct
answer.
|
|
|
21.
|
Find 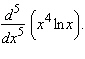 Select the correct answer.
|
|
|
22.
|
Find the limit. 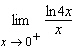 Select the correct
answer.
|
|
|
23.
|
Evaluate the integral. 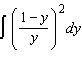 Select the correct
answer.
|
|
|
24.
|
Find the limit. 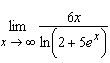 Select the correct
answer.
|
|
|
25.
|
Use l'Hospital's Rule to calculate the exact value of the limit as
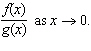 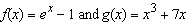 Select the correct answer.
|
|
|
26.
|
Graph the region between the curves and use your calculator to compute the area
correct to five decimal places. 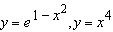 Select the correct answer. a. | 3.14134 | b. | 3.66016 | c. | 7.32031 | d. | 7.38905 | e. | none of
these |
|
|
|
27.
|
Differentiate the function. 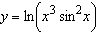 Select the correct
answer.
|
|
|
28.
|
Find 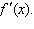 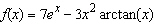 Select the correct
answer.
|
|
|
29.
|
For the period from 1980 to 2000, the percentage of households in the United
States with at least one VCR has been modeled by the function 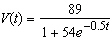 where the time
t is measured in years since midyear 1980, 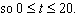 Use derivatives to estimate the
time at which the number of VCRs was increasing most rapidly. Select the correct answer.
|
|
|
30.
|
The geologist C. F. Richter defined the magnitude of an earthquake to be 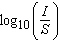 where I is the intensity of the quake (measured by the amplitude of a seismograph
100 km from the epicenter) and S is the intensity of a ”standard” earthquake
(where the amplitude is only 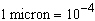 cm). The 1989 Loma Prieta earthquake that shook
San Francisco had a magnitude of 7.1 on the Richter scale. The 1906 San Francisco earthquake was 16
times as intense. What was its magnitude on the Richter scale? Select the correct answer.
a. | 113.6 | b. | 8.3 | c. | 8.5 | d. | 8.4 | e. | 124 |
|
|
|
31.
|
Use logarithmic differentiation to find the derivative of the function.
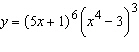 Select the correct answer.
|
|
|
32.
|
Evaluate the integral. 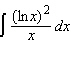 Select the correct
answer.
|
|
|
33.
|
Find the derivative of y. 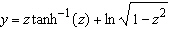 Select the
correct answer.
|
|
|
34.
|
Graph the region between the curves and use your calculator to compute the area
correct to five decimal places. 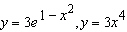 Select the correct answer. a. | 3.66016 | b. | 3.14134 | c. | 7.38905 | d. | 10.98047 | e. | 7.38915 |
|
|
|
35.
|
If 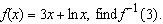 Select the correct answer.
|
|
|
36.
|
Find the limit. 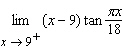 Select the correct
answer.
|
|
|
37.
|
A painting in an art gallery has height h and is hung so that lower edge
is a distance d above the eye of an observer (as in the figure). How far from the wall should
the observer stand to get the best view? (In other words, where should the observer stand so as to
maximize the angle 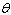 subtended at his eye by the painting?)
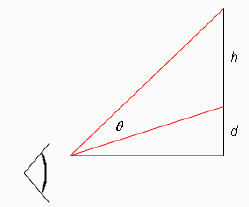 Select the correct answer.
|
|
|
38.
|
A lighthouse is located on a small island, 3 km away from the nearest point P
on a straight shoreline, and its light makes six revolutions per minute. How fast is the beam of
light moving along the shoreline when it is 1 km from P?
Select the correct answer.
|
|
|
39.
|
Use the definitions of the hyperbolic functions to find the following limit.
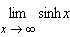 Select the correct answer.
|
|
|
40.
|
Find 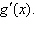 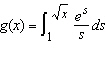 Select the correct
answer.
|
|
|
41.
|
A telephone line hangs between two poles at 12 m apart in the shape of the
catenary 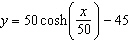 , where x and y are measured in
meters. Find the slope of this curve where it meets the right pole. 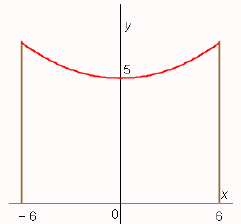 Select the correct answer. a. | 0.1203 | b. | 0.8962 | c. | 0.4888 | d. | 0.8079 | e. | 0.1389 |
|
|
|
42.
|
Find the limit. 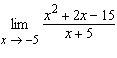 Select the correct
answer.
|
|
|
43.
|
Evaluate the integral. 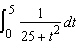 Select the correct
answer. a. | 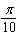 | b. | 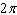 | c. | 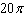 | d. | 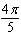 | e. | 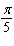 | f. | none of
these |
|
|
|
44.
|
Find the limit. 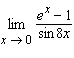 Select the correct
answer.
|
|
|
45.
|
Find the average value of the function on the given interval. 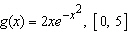 Select the correct answer.
|
|
|
46.
|
Evaluate the integral. 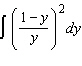 Select the correct
answer.
|
|
|
47.
|
Evaluate the integral to three decimal places. 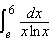 Select the correct answer. a. | 0.194 | b. | 0.533 | c. | 0.183 | d. | 0.583 | e. | 0.094 |
|
|
|
48.
|
Find the average value of the function on the given interval. 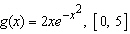 Select the correct answer.
|
|
|
49.
|
If 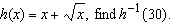 Select the correct answer.
|
|
|
50.
|
Suppose that the graph of 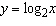 is drawn on a coordinate grid
where the unit of measurement is an inch. How many miles to the right of the origin do we have to
move before the height of the curve reaches 2 ft. Select the
correct answer. a. | 66.99 mi | b. | 409.37 mi | c. | 202.56
mi | d. | 264.79 mi | e. | 609.99 mi |
|
|
|
51.
|
Solve the inequality. 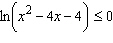 Select the correct
answer.
|
|
|
52.
|
Differentiate the function. 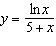 Select the correct
answer.
|
|
|
53.
|
Use logarithmic differentiation to find the derivative of the function.
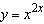 Select the correct answer.
|
|
|
54.
|
Find the limit. 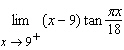 Select the correct
answer.
|
|
|
55.
|
Find 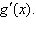 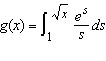 Select the correct
answer.
|
|
|
56.
|
Evaluate the integral. 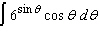 Select the correct
answer.
|
|
|
57.
|
If f is a one-to-one function such that f(6) = 1, what is 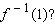 Select the correct answer.
|
|
|
58.
|
Determine f(x) from the table. The values from the table are given to the
nearest ten thousandth. 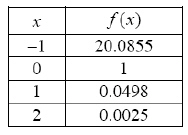 Select the correct answer.
|
|
|
59.
|
Find the inverse of the function. 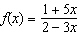 Select the
correct answer.
|
|
|
60.
|
Differentiate the function. 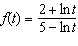 Select the correct
answer.
|
|
|
61.
|
Find the average value of the function on the given interval. 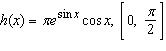 Select the correct answer.
|
Numeric Response
|
|
|
62.
|
Use the properties of logarithms to expand the quantity.
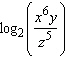 __________
|
|
|
63.
|
Find the solution of the equation correct to four decimal places. 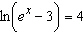 __________
|
|
|
64.
|
Suppose that the graph of 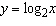 is drawn on a coordinate grid
where the unit of measurement is an inch. How many miles to the right of the origin do we have to
move before the height of the curve reaches 3 ft. Give the answer to two decimal places.
__________
|
|
|
65.
|
Use logarithmic differentiation to find the derivative of the function.
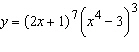 __________
|
|
|
66.
|
If a bacteria population starts with 50 bacteria and doubles every three hours,
then the number of bacteria after t hours is 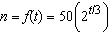 . When will the population reach
60,000? __________
|
|
|
67.
|
Differentiate the function. 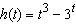 __________
|
|
|
68.
|
Graph the region between the curves and use your calculator to compute the area
correct to five decimal places. 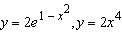 __________
|
|
|
69.
|
Differentiate the function. 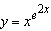 __________
|
|
|
70.
|
Evaluate the integral. 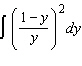 __________
|
|
|
71.
|
Find 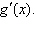 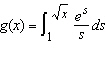 __________
|
|
|
72.
|
Solve each equation for x.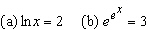 ___________
|
|
|
73.
|
Evaluate the integral. 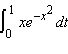 __________
|
|
|
74.
|
Use logarithmic differentiation to find the derivative of the function.
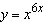 __________
|
|
|
75.
|
Find the volume of the solid obtained by rotating the region bounded by the
given curves about the specified line. 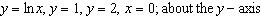 ___________
|
|
|
76.
|
Find 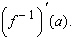 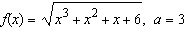 __________
|
|
|
77.
|
If 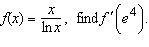 __________
|
|
|
78.
|
Differentiate the function. 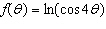 __________
|
|
|
79.
|
Find the derivative of the function. 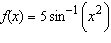 __________
|
|
|
80.
|
If 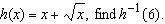 __________
|
|
|
81.
|
Graph the region between the curves and use your calculator to compute the area
correct to five decimal places. 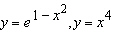 __________
|
|
|
82.
|
Find the limit. 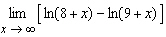 __________
|
|
|
83.
|
Differentiate the function. 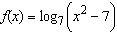 __________
|
|
|
84.
|
Find the exact value of the expression. 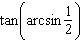 __________
|
|
|
85.
|
Suppose g is the inverse function of a differentiable function f
and 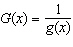 . If 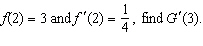 __________
|
|
|
86.
|
If 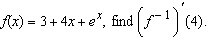 __________
|
|
|
87.
|
Use transformations to sketch the graph of the function. 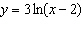 __________
|
|
|
88.
|
Differentiate the function. 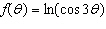 __________
|
|
|
89.
|
Differentiate the function. 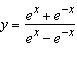 __________
|
|
|
90.
|
Find the values of 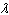 for which 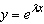 satisfies the
equation 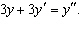 __________
|
|
|
91.
|
Evaluate the integral. 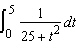 __________
|
|
|
92.
|
Find the average value of the function on the given interval. 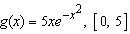 __________
|
|
|
93.
|
Use a computer algebra system to find the exact volume of the solid obtained by
rotating the region bounded by the given curves about the specified line. 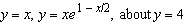 __________
|
|
|
94.
|
Suppose g is the inverse function of a differentiable function f
and 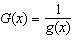 . If 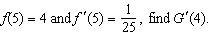 __________
|
|
|
95.
|
If 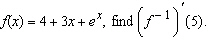 __________
|
|
|
96.
|
Use logarithmic differentiation to find the derivative of the function.
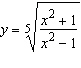 __________
|
|
|
97.
|
Find the exponential function 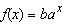 whose graph is
given. 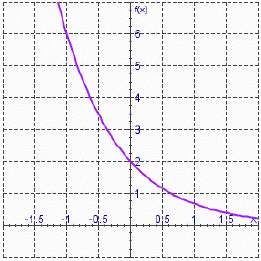 __________
|
|
|
98.
|
Solve the equation for x.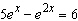 ___________
|
|
|
99.
|
Evaluate the integral. 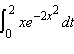 __________
|
|
|
100.
|
Differentiate the function. 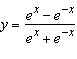 __________
|
|
|
101.
|
Find the values of 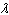 for which 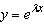 satisfies the
equation 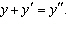 __________
|
|
|
102.
|
Differentiate the function. 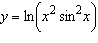 __________
|
|
|
103.
|
If a bacteria population starts with 100 bacteria and doubles every three hours,
then the number of bacteria after t hours is 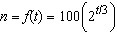 . When will the population reach
50,000? __________
|
|
|
104.
|
Find 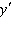 if 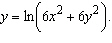 __________
|
|
|
105.
|
Find, correct to three decimal places the area of the region above the hyperbola
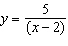 , below the x axis, and between the lines x = – 4 and x =
– 3. __________
|
|
|
106.
|
Find an equation of the tangent line to the curve 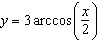 at the point 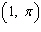 . ___________
|
|
|
107.
|
Evaluate the integral. 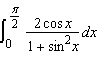 __________
|
|
|
108.
|
Find the limit. 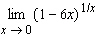 __________
|
|
|
109.
|
Use l'Hospital's Rule to calculate the exact value of the limit as
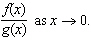 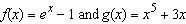 __________
|
|
|
110.
|
Find the inverse function. 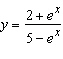 __________
|
|
|
111.
|
Use transformations to sketch the graph of the function. 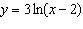 __________
|
|
|
112.
|
Suppose g is the inverse function of a differentiable function f
and 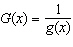 . If 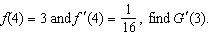 __________
|
|
|
113.
|
Find the solution of the equation correct to four decimal places. 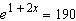 __________
|
|
|
114.
|
Graph the region between the curves and use your calculator to compute the area
correct to five decimal places. 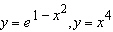 __________
|
|
|
115.
|
Find the limit. 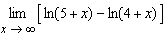 __________
|
|
|
116.
|
Find the volume of the solid obtained by rotating about the y axis the
region bounded by the curves. 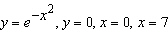 ___________
|
|
|
117.
|
Evaluate the integral. 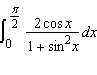 __________
|
|
|
118.
|
If 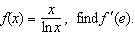 __________
|
|
|
119.
|
If a bacteria population starts with 150 bacteria and doubles every 7 hours,
then the number of bacteria after t hours is 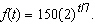 When will the population reach
10,000? __________
|
|
|
120.
|
Find the derivative of 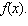 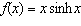 __________
|
|
|
121.
|
Find the values of 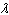 for which 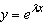 satisfies the
equation 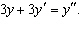 __________
|
|
|
122.
|
Solve each equation for x.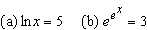 ___________
|
|
|
123.
|
Find the solution of the equation correct to four decimal places. 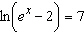 __________
|
|
|
124.
|
Differentiate the function. 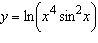 __________
|
|
|
125.
|
If 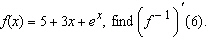 __________
|
|
|
126.
|
Find an equation of the tangent line to the curve at the given
point. 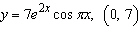 ___________
|
|
|
127.
|
Find the absolute minimum value of the function.
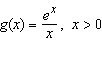 __________
|
|
|
128.
|
If a bacteria population starts with 150 bacteria and doubles every three hours,
then the number of bacteria after t hours is 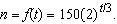 When will the population reach
45,000? __________
|
|
|
129.
|
Suppose that the graph of 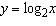 is drawn on a coordinate grid
where the unit of measurement is an inch. How many miles to the right of the origin do we have to
move before the height of the curve reaches 3 ft.
__________
|
|
|
130.
|
Use logarithmic differentiation to find the derivative of the function.
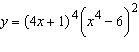 __________
|
|
|
131.
|
Find the average value of the function on the given interval. 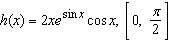 __________
|
|
|
132.
|
If 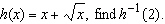 __________
|
|
|
133.
|
Find 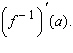 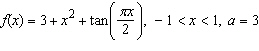 __________
|
|
|
134.
|
Find the limit. 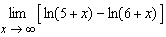 __________
|
|
|
135.
|
Suppose g is the inverse function of a differentiable function f
and 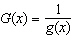 . If 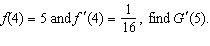 __________
|
|
|
136.
|
Differentiate the function. 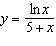 __________
|
|
|
137.
|
Differentiate the function. 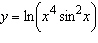 __________
|
|
|
138.
|
If 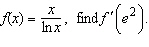 __________
|
|
|
139.
|
Find 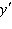 if 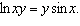 __________
|
|
|
140.
|
Use logarithmic differentiation to find the derivative of the function.
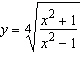 __________
|
|
|
141.
|
Evaluate the integral to three decimal places. 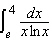 __________
|
|
|
142.
|
If a bacteria population starts with 100 bacteria and doubles every three hours,
then the number of bacteria after t hours is 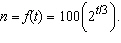 When will the population reach
50,000? __________
|
|
|
143.
|
Find the limit. 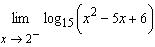 __________
|
|
|
144.
|
Differentiate the function. 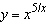 __________
|
|
|
145.
|
Evaluate the integral. 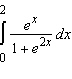 __________
|
|
|
146.
|
Evaluate the integral. 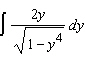 __________
|
|
|
147.
|
Evaluate the integral. 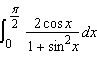 __________
|
|
|
148.
|
Use a computer algebra system to find the exact volume of the solid obtained by
rotating the region bounded by the given curves about the specified line. 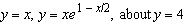 __________
|
|
|
149.
|
Solve each equation for x.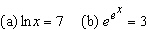 ___________
|
|
|
150.
|
Find 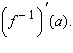 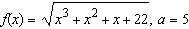 __________
|
|
|
151.
|
Differentiate the function. 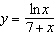 __________
|
|
|
152.
|
Use transformations to sketch the graph of the function. 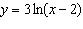 __________
|
|
|
153.
|
Differentiate the function. 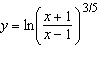 ____________
|
|
|
154.
|
Evaluate the integral. 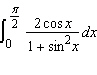 __________
|
|
|
155.
|
Evaluate the integral to three decimal places. 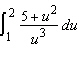 __________
|
|
|
156.
|
Evaluate the integral to three decimal places. 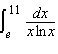 __________
|
|
|
157.
|
Differentiate the function. 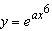 __________
|
|
|
158.
|
Differentiate the function. 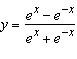 __________
|
|
|
159.
|
Evaluate the integral. 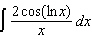 __________
|
|
|
160.
|
Find the volume of the solid obtained by rotating the region bounded by the
given curves about the specified line. 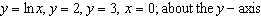 ___________
|