- I'm sure that you've been emailed about evaluations. Please take
some time to fill those out. I (and professors generally) find
them useful, especially the written comments.
- Your final assignment is due: what questions do you have about it?
- Final exam: This Monday, April 30th, 10:10 a.m. - 12:10 p.m.
- You may have a sheet of notes, one-page, front and back.
- Linear Systems
- We started with an interesting problem: balancing a
chemical reaction. That problem had a solution -- but,
moreover, it had an infinite number of
solutions.
The equations were linear, meaning that we could write equations relating the quantities of interest in the form
- The question we began with was this: is there a solution, and, provided there is, is it unique? Turns out that those are the three possibilities.
- We examined the geometric meaning of these three
possibilities, which we can represented well in the
two-dimensional
case:
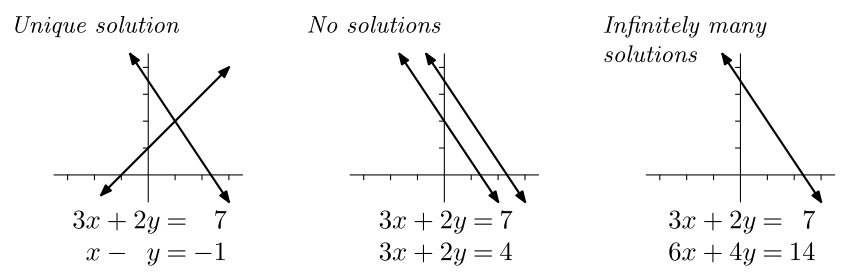
In higher dimensions, the situation is analogous: three planes intersecting (or not), etc.
- This issue was raised when we did our linear regression
projects. Because we had many equations in only a few unknowns,
it's unlikely that we'll be able to find a solution.
For example, if you have 10 items on which you measure two variables for each item, then it's like trying to find a unique intersection of 10 planes. Good luck!
So we replaced the given rectangular system with a square system, and hoped that it would possess a solution.
- We defined an angle between vectors, which we could calculate via the dot (or inner) product. This product allowed us to compute lengths of vectors (the norm), and test for perpendicularity.
- We discovered how to write equations of planes and lines using these notions.
- Then we discussed the Gauss reduction steps:
- Row swaps
- Row scalings
- Linear combinations of a row with another.
- Gauss-Jordan meant that we would reduce down to a matrix with either ones or zeros on the main diagonal, and zeros elsewhere.
- We started with an interesting problem: balancing a
chemical reaction. That problem had a solution -- but,
moreover, it had an infinite number of
solutions.
- Vector Spaces
- This section takes a different approach to solving linear systems. We phrase the question of a solution a little differently.
- We have these things called vectors. We create operations by which we can add them, and scale them. Then we impose rules on the vector operations.
- The result is something called a vector space. Any objects on which these operations of addition and scaling can be defined to satisfy the rules gives us a vector space.
- This allows us to talk about vector spaces of directed arrows, but also vector spaces of functions, matrices, real numbers, etc.
- So the operations of adding vectors ("arrows") in three space, butt to tip, or stretching or shrinking vectors can be talked about in the context of functions, or matrices, or....
- We can even talk about the angle between two polynomials, for example, by computing a dot product! Seems strange, but is ultimately useful.
- So what's the "new approach" to a solution of a linear
system? We think of a system as a matrix equation,
will be the coefficients of a linear combination of the column vectors of A that equals the vector
.
- We ask this: "Is
in the column space of A?"
- The columns of A form a vector space, and the
question is whether the columns of A (which span
the column space) can generate the vector
.
- We also discovered that the rows form a vector space, defined the dimension of a vector space (as the size of a basis -- that is, a set of vectors that is linearly independent and also spans the space), and discovered that the dimensions of the column and row spaces were the same.
- One question that one might ask at this point is "which basis might be best?"
- Maps Between Spaces
- This chapter begins with the notion of an isomorphism
between vector spaces. Under what conditions can one map a
space right onto another space via map f so that
- each vector of each space has a unique partner in the other space, and
- the operations a preserved, in the sense that f preserves linear combinations:
- We saw that there are certain obvious examples of such
things. If we think of the plane, represented by
, then some obvious examples include
- rotations of the plane about the origin,
- inflations or deflations of the space from the origin,
- reflections through the origin.
- These examples are examples of an even more specific kind of isomorphism, called and automorphism (an isomorphism between a space and itself).
- This allows us to
- Then we generalized the notion of isomorphism, considering homomorphisms (maps between vector spaces which merely preserve linear combinations).
- We found that homomorphisms can be represented by matrices
-- but the form of the matrix depends on the bases in which
both the domain and codomain are expressed.
If we change either basis, the matrix representation H of the homomorphism h will change.
- Similarly we discovered that a matrix represents a homomorphism -- or rather an infinite number of different homomorphisms -- again, it depends on the bases used.
- So we practiced representing a homomorphism in different bases. In the end we ask the same old question: is there some especially good basis in which to represent the map?
- We considered those special matrices which represent the
inverse of an isomorphism. Starting from a given matrix
representation H of invertible homomorphism h, we
discovered how to compute some simple inverse matrices
(the 2x2 case, diagonal matrices).
- This chapter begins with the notion of an isomorphism
between vector spaces. Under what conditions can one map a
space right onto another space via map f so that
- Determinants
- Matrices in this section are assumed square, since we're considering invertibility.
- I suggested that we focus our understanding of
Determinants on three things:
- The job(s) determinants do
- One method of calculating determinants
- The geometric interpretation of the determinant.
- A determinant of 0 tell us if a matrix is singular (that is, not invertible).
- We can compute determinants by the method of cofactor expansion (due to Laplace) -- successively computing determinants of smaller dimension, and so working our way down to the 2x2 case which is elementary ("ad-bc").
- Homomorphisms tranform circles into ellipses, spheres into ellipsoids, hyperspheres into hyperellipsoids, etc. Whatever the ball is in n dimensions, it gets squished into an ellipsoidal ball in n dimensions.
- One geometric interpretation of the determinant is that it is the "space expansion" factor of the transformation: when a ball of unit volume gets transformed into an ellipsoid, its volume expands or contracts by a factor of det(A).
- Similarity
- Eigenvalue and Eigenvectors are the focus of this chapter. A transformation h may have special vectors whose images under the transformation are especially simple: just scalar multiples of themselves.
- Such vectors would satisfy an equation of the form
- The values
are called the eigenvalues (one associated with each eigenvector).
- Finding a set of these eigenvectors would allow us to
diagonalize a matrix: that is, we seek a matrix B
so that
where the elements of the diagonal matrix
are the eigenvalues
.
- Such a matrix B (whose columns are the
eigenvectors,
) is an ideal basis in which to represent the transformation h.
- Applications included population dynamics, and the calculation of the Fibonacci numbers.
- One thing that we discovered is that it is easy to compute
powers of matrix H if we can diagonalize it:
We used this trick to write the Fibonacci number
in closed form, as