Day 14, MAT115

• The New York Times just had Monte Hall on its Science page on Tuesday!
• By the way: most of you should avoid gambling....
• Did anyone try Fibonacci Nim with someone? Win anything interesting?

• Rules:
  • There are two players, Player 1 and Player 2. Player 1 will go first.
  • An arbitrary number of counters is thrown down (e.g. toothpicks, pennies).
  • Player 1 must pick up at least one counter, but may not pick up all the counters.
  • Player 2 must then pick up at least one counter, and not more than twice the number of counters picked up on Player 1's turn.
  • The players continue taking turns, subject to these same conditions: pick up at least one, no more than twice what the preceding player took.
  • The player who picks up the final counter wins.
• Let's play a sample game: Suppose that there are 27 counters on the table.
• You play a sample game with a partner: Suppose that there are 43 counters on the table.

• Start with a new-born pair of "immortal" bunnies (they never die).
• A new-born pair requires a month to mature.
• The following month, the pair produces a new pair, which is subject to the same rules.
• Do it again, do it again, do it again!

The Fibonacci numbers have a number of interesting properties. Let's investigate one, as mathematicians do, by searching for a pattern:

By experimenting with numerous examples in search of a pattern, determine a simple formula for

that is, a formula for the sum of the squares of two consecutive Fibonacci numbers. Try various values of n (at least five different values) to see what happens.

Every natural number is either

1. Fibonacci, or
2. can be written as a sum of non-consecutive Fibonacci's in a unique way.

Examples?

• If you looked at some special cases, what can we conclude?

  Number of sticks	1	2	3	4	5	6	7	8
  Winner	X	P2	P2	P1	P2	P1	P1	P2

  We noticed that the places where P2 wins are 2, 3, 5, 8, and from that we noticed a pattern: the Fibonacci numbers.

• So what's the winning strategy in Fibonacci Nim? Two cases:
  1. If the number of counters is Fibonacci, you want to be player 2.
  2. If the number of counters is not Fibonacci, you want to be player 1, and write the number as a sum of non-consecutive Fibonacci numbers, taking the smallest Fibonacci number of counters.
  If you find yourself in the wrong position, play a slow-down strategy -- take 1. You'll have to hope that your competition makes a mistake, and puts you back in the driver's seat.

• Put your page in "Landscape mode" (long side left and right)
• Darken the square 10 from the left, and 6 down.
• Adjoin the largest square we can to the first square, still making a rectangle (that is, darken the square to the left of the first one)
• Now adjoin the largest square to the rectangle created, still making a rectangle, and do so in one single direction -- counter-clockwise in this case (that's a 2x2 square, below the rectangle you created in the first two steps).
• Now we're going to "do it again, do it again"!

• Let's look at some pine cones....
• dandelions (Here's a scanned dandelion)
• Spirals in daisies:
  • 21 spirals
  • 34 spirals
  • together
• Similar things happen in artichokes, pineapples, etc.

• "The Sexiest Rectangle" - or is it just cute?
  • Important property: if you cut out the largest square possible, you still have a golden rectangle! There's a "world within a world" in the golden rectangle....

  • The golden mean (or golden ratio, golden section) -- A "precious jewel" (Johannes Kepler)
    • derived by ratios of Fibonacci numbers, or
    • using the rectangle directly. The Greeks defined a golden rectangle by calling it the rectangle which, when the largest square possible is removed, retains its shape (which means that the ratio of side lengths doesn't change).
    • The golden rectangle has side lengths in the ratio

      Note that the value is only approximately 1.618: is an irrational number, like , and its decimal representation goes on forever and never repeats:

      

• Now: what kind of rectangle will you get if you repeat the Fibonacci spiral process with another kind of rectangle to start (rather than a square)?

  Turns out, that if you do it over and over and over again, you'll get a rectangle that gets more and more golden.

  Let's try: we'll use a piece of grid paper (looking short and squat), and a 3x1 rectangle (start it running the tall-way at the 12th row down, 8th cell over).

  Now, let's figure out what the recurrence relation is for the dimensions of our rectangles, and then figure out if we're getting golden....

• The A0 Paper Fractal

  "A paper" is something you've no doubt encountered before: it's the long sheets we occasionly use (usually "A4" paper), which is far more common in Europe.

  "A paper" is constructed so that, if folded in half (do we say the long way or the short way?), you get a sheet which has exactly the same shape -- that is, the ratio of its side lengths is the same as the original sheet.

  

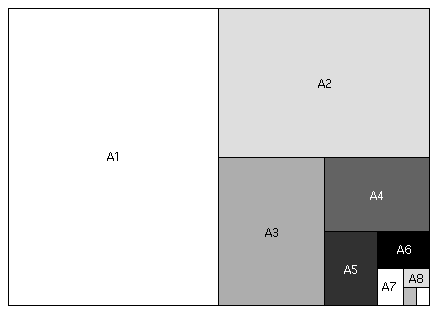
  Let's see what the dimensions of A paper must be so that this requirement is fulfilled....

  Call the long dimension of the A1 paper above , and the short dimension 1.

  • Then what are the dimensions of the A2 paper, according to the design of A paper?
  • What is the value of ?

• Why not an A0 paper spiral? Let's try that.... This is the spiral, created using non-squares each time:
  

  In both cases there's "the world within the world". Both are fractals.