- Enjoy your fall break!
- You have a homework due today.
- You have a new homework assignment, which will be due on Tuesday 10/21, following the break.
- Before we go on today, let's check out a little binary hand dancing....
Today we're going to review the golden rectangle and Pascal's triangle; then investigate Pascal's a little more, to find another number pattern within. Then we'll take another glance back at the Fibonacci spiral, and a look forward to the world of fractals, which we'll be encountering soon.
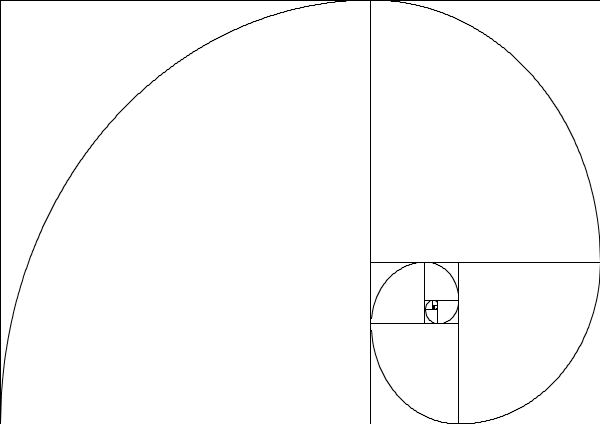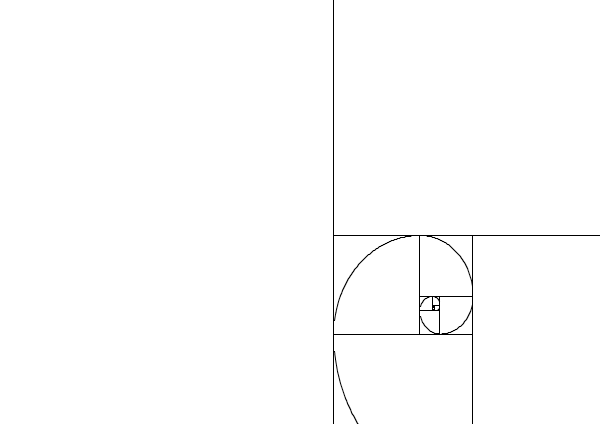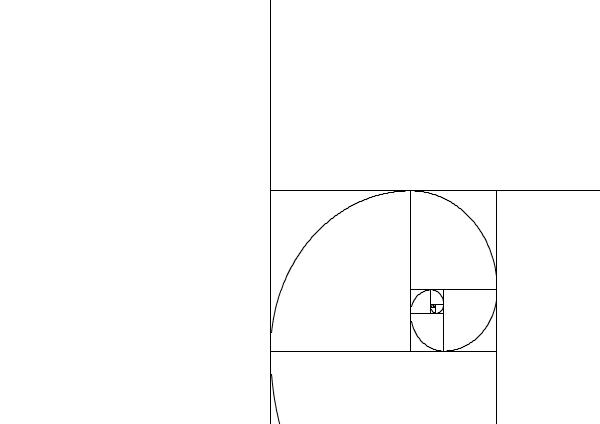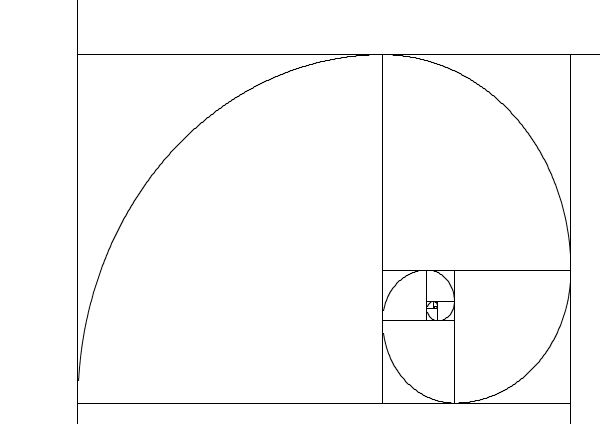
- "The Sexiest Rectangle" - or is it just cute?
- Important property: if you cut out the largest square
possible, you still have a golden rectangle! There's a "world
within a world" in the golden rectangle....
- The golden mean (or golden ratio, golden section) -- A
"precious jewel" (Johannes Kepler)
- derived by ratios of Fibonacci numbers, or
- using the rectangle directly. The Greeks defined a golden rectangle by calling it the rectangle which, when the largest square possible is removed, retains its shape (which means that the ratio of side lengths doesn't change).
- The golden rectangle has side lengths in the ratio
Note that the value is only approximately 1.618:
is an irrational number, like
, and its decimal representation goes on forever and never repeats:
- Important property: if you cut out the largest square
possible, you still have a golden rectangle! There's a "world
within a world" in the golden rectangle....

This will allows us to do is to understand how this Chinese culture of the 13th century wrote its numbers (Chinese Bamboo Counting Rods). How did these people write 15? 28? 30?
This is a famous bit of mathematics that some of you may recognize, and we'll study it more on its own right soon.
Interestingly enough, there's a mistake in one row of the Chinese version of this table.
Here's an updated hexagonal version of Pascal's triangle. This one is particularly useful for showing the method for generating all the Fibonacci numbers from the table:

The claim is that there is some relationship between Pascal's triangle and the binary numbers. Let's use the simplified version below to discover this relationship.

So why does this happen? There's a nice way to think about this relationship. We need to understand a concept of sets, however. This concept is very important, and is actually the reason that Pascal was interested in it.
Here's the question Pascal's triangle answer: for a set of objects, say four objects, how many ways can one create subsets of the objects? What kinds of subsets are there, and how many are there of each type? Rather than objects, think of students.
If there are two cars and four students, in how many different ways can we put students into the cars?
- This triangle is much older than Blaise
Pascal, who lived in the 17th century (it dates also to
China, long before -- 13th century AD). But the Indians were
considering it as early as the 4th center BCE (Pingala).
Here's how a 10th century AD manuscript described Pingala's approach to the constructing the triangle:
"Draw a square. Beginning at half the square, draw two other similar squares below it; below these two, three other squares, and so on. The marking should be started by putting 1 in the first square. Put 1 in each of the two squares of the second line. In the third line put 1 in the two squares at the ends and, in the middle square, the sum of the digits in the two squares lying above it. In the fourth line put 1 in the two squares at the ends. In the middle ones put the sum of the digits in the two squares above each. Proceed in this way. Of these lines, the second gives the combinations with one syllable, the third the combinations with two syllables, ..."
- While we don't have the BCE Indian version of the table, we do have a
version from a Jewish mathematician who converted to Islam (and used Arabic numerals -- thanks Mark Middendorf for the graphic):
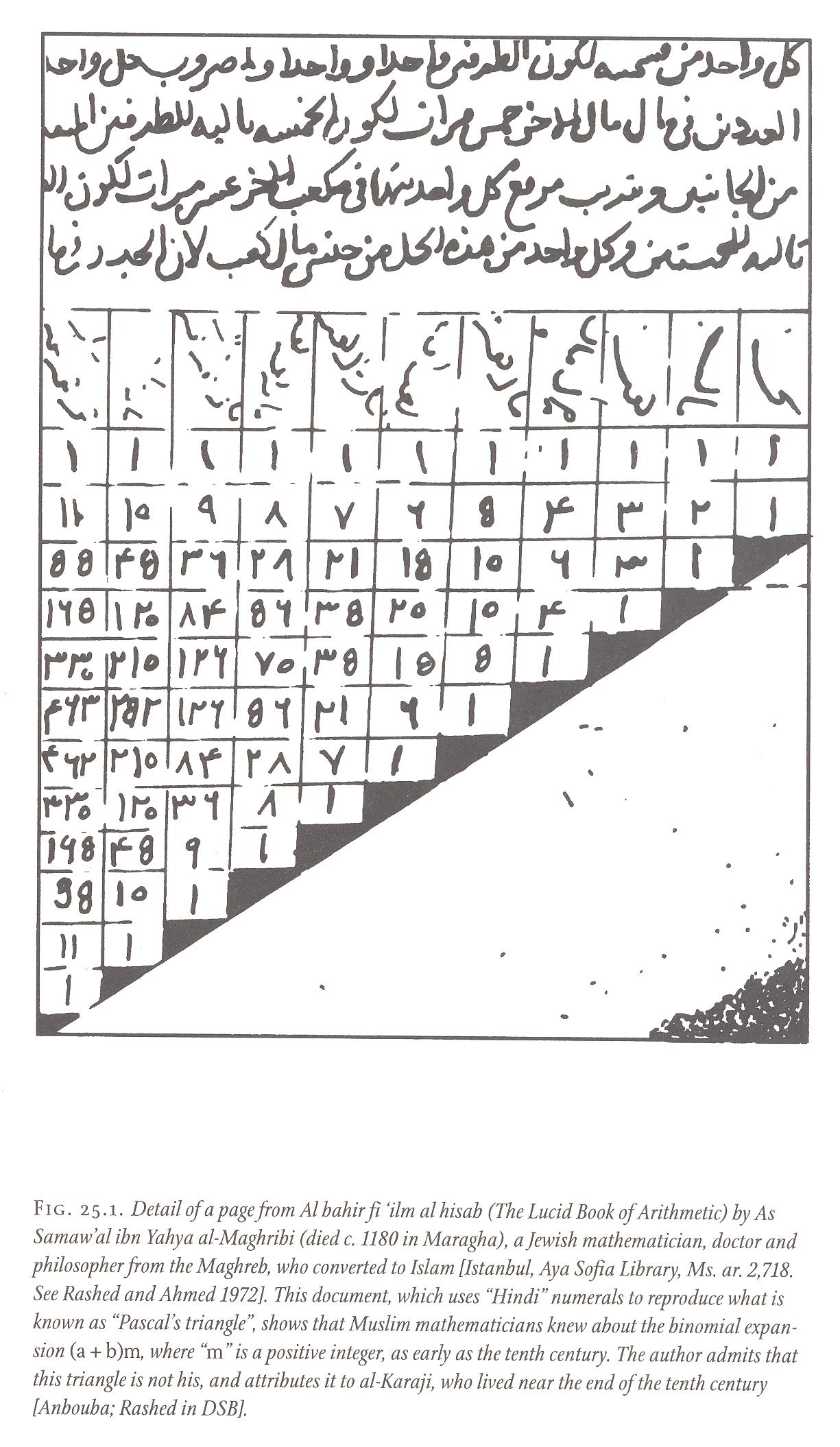
(from the marvellous book The Universal History of Numbers, by Georges Ifrah). - Let's see how Vi Hart plays games with Pascal's triangle....
- Now: what kind of rectangle will you get if you repeat the
Fibonacci spiral process with another kind of rectangle to
start (rather than a square)?
Turns out, that if you do it over and over and over again, you'll get a rectangle that gets more and more golden.
Let's try: we'll use a piece of grid paper (looking "tall"), and a 3x1 rectangle (start it running the tall-way at the 5th row down, 8th cell over). For the next two steps, go "right", "up".
Now, let's figure out what the recurrence relation is for the dimensions of our rectangles, and then figure out if we're getting golden....
- The A0
Paper Fractal
"A paper" is something you've no doubt encountered before: it's the long sheets we occasionly use (usually "A4" paper), which is far more common in Europe.
"A paper" is constructed so that, if folded in half (do we say the long way or the short way?), you get a sheet which has exactly the same shape -- that is, the ratio of its side lengths is the same as the original sheet.
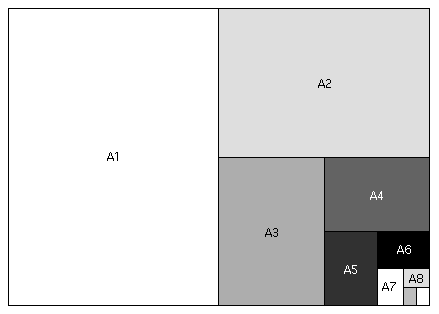
Let's see what the dimensions of A paper must be so that this requirement is fulfilled....
Call the long dimension of the A1 paper above
, and the short dimension 1.
- Then what are the dimensions of the A2 paper, according to the design of A paper?
- What is the value of
?
- Why not an A0 paper spiral? Let's try that....
This is the spiral, created using non-squares each time:
As you can see there's "a world within a world". This is a fractal, as is this spiraling version of the Fibonacci spiral: