- An important reminder: your logos are due in exactly two
weeks. Here are some examples. Yours
should be different! You will have two to three minutes to describe
your logo. It should be printed off, or emailed to me ahead of
time. Next week I will establish an order in which the logos will be
presented.
Remember that "You will type up a one-page sheet, illustrating and explaining your choice."
These were originally to be presented on the last day of class, but, because I'll be out of town on Tuesday (and I have to be here for the review), I switched those days.
- Your homework on the
"Knotty Tale" is due today, but I'll take it
Thursday if you haven't gotten it figured out. We'll be doing some more
practice today, which may help.
- You have another homework due next time (on knots).
- You also have an assignment due next Tuesday.
- A famous mathematician just died, Alexander
Grothendieck:

"If there is one thing in mathematics that fascinates me more than anything else (and doubtless always has), it is neither `number' nor `size,' but always form," he wrote in a long memoir in the 1980s, "Reapings and Sowings." "And among the thousand-and-one faces whereby form chooses to reveal itself to us, the one that fascinates me more than any other and continues to fascinate me, is the structure hidden in mathematical things." We have been studying the structure hidden in mathematical things!
- The use of knot tiles and knot mosaics was partly inspired by a talk I
saw on Quantum Knots.
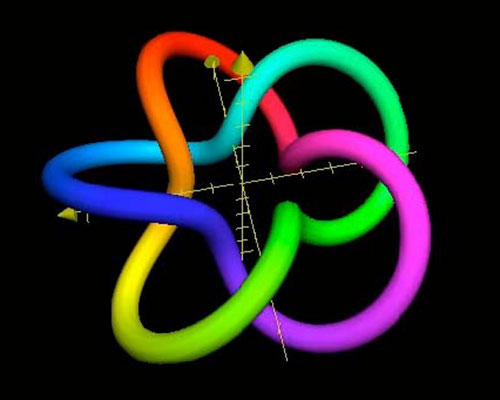
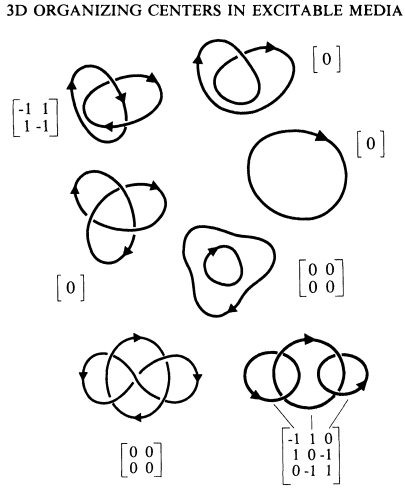
- Trefoil knots are in your heart
(the following images are from a paper by Art Winfree at the University
of Arizona, on "excitable media"):
-
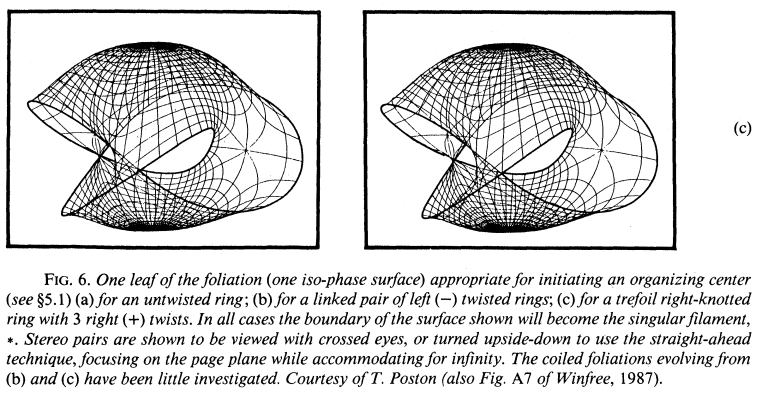
- My dad carved mathematical objects, including this surface for Art Winfree (related to heart arrhythmias):
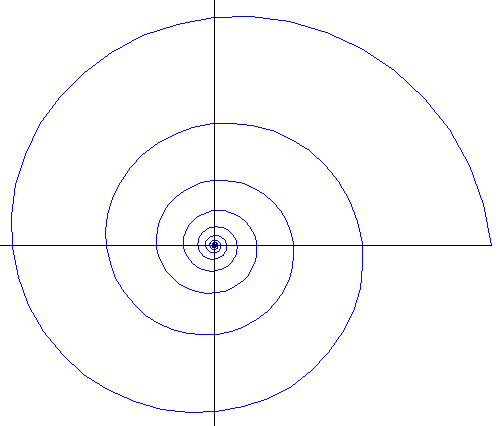
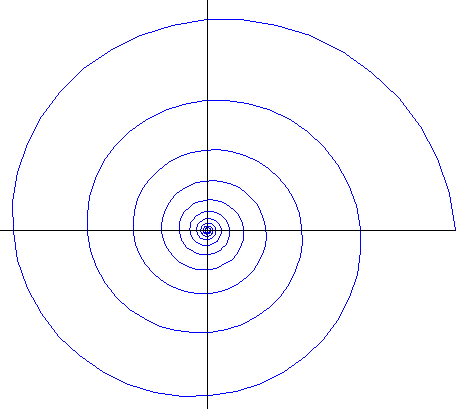
- I just received a copy of Science News. On the cover was a shell,
I had my son Thad help me with the calculations of the changes in the spiral arms.
The shell is not Fibonacci. The Fibonacci spiral rings grow as the golden mean to the fourth power,
:
My son measured the distance of successive rings from the center of the shell, and found that each successive ring is about 1.87 times the preceding one. This gives rise to the shell on the left (a "golden" 1.618 shell is on the right):
- In the same issue of Science News there was a story about Mayan
Kings, and there was a picture of a piece of carved Jade found in the
tomb of one of them:

At first I thought that the four sides were the same, and I got this link of four separate strands:

Then I realized that two sides were shorter, and I got this royal link of six separate strands:
- I'm reading Malcolm Gladwell's book The Tipping Point:
p. 178: "Dunbar's argument is that brains evolve, they get bigger, in
order to handle the complexities of larger social groups. If you belong
to a group of five people, Dunbar points out, you have to keep track of
ten separate relationships: your relationships with the four others in
your circle and the six other two-way relationships between the
others.... If you belong to a group of twenty people, however, there
are now 190 two-way relationships to keep track of: 19 involving
yourself and 171 involving the rest of the group."
Question for you: where do those numbers come from?
The interesting conclusion of this research is evidently that 150 people is the ideal size of an organization. Much bigger than that, and we start to develope "cliques".
- Thad wondered how many presents were given out by "my true love"
during the "12 Days of Christmas". It's a trapezoidal number!
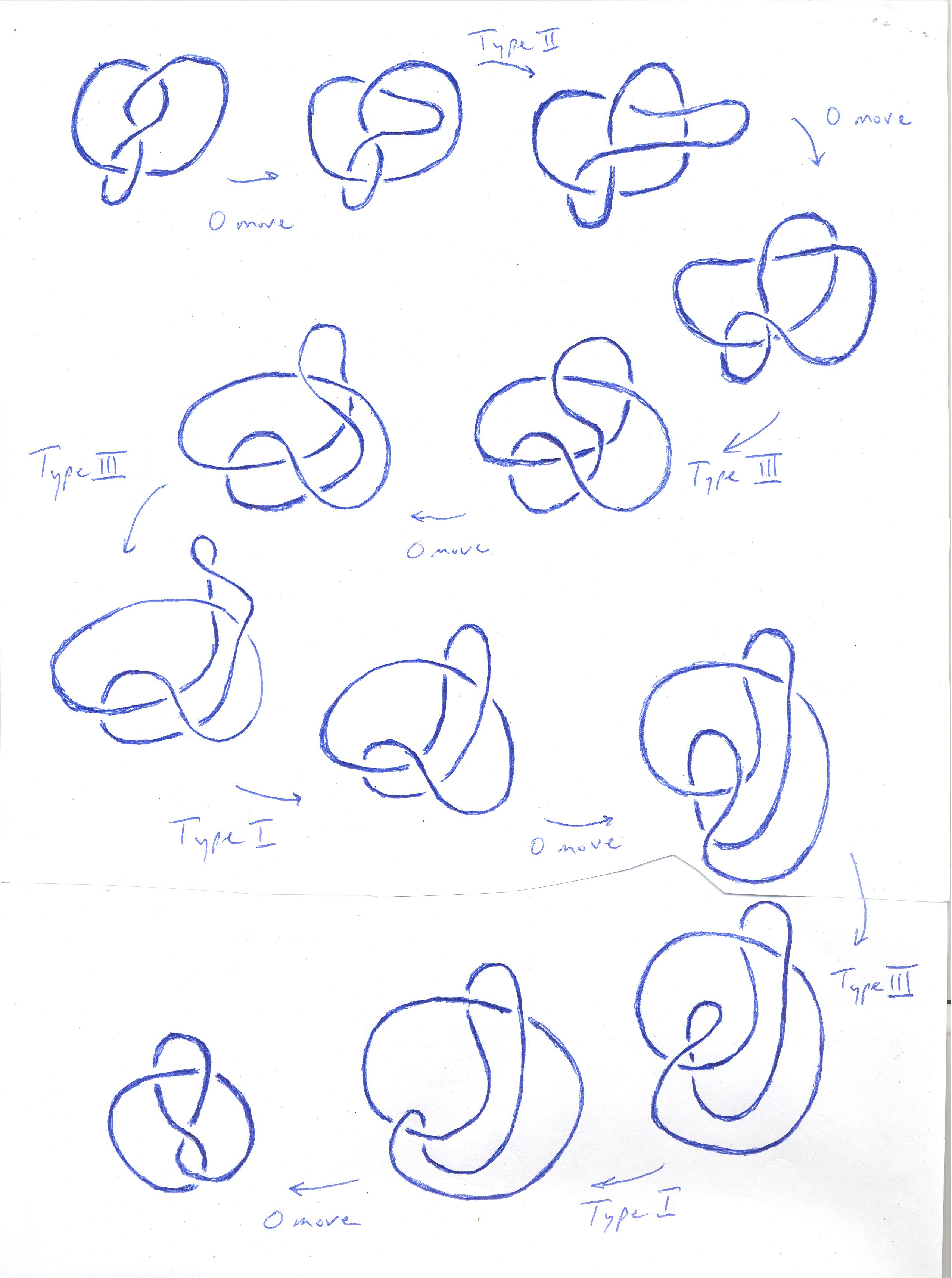
- Last time we looked at an illustration showing that the
figure-eight knot is equivalent to its mirror image, but I wasn't able
to follow the diagram in places:

(from A figure-eight knot is equivalent to its mirror reflections: I'm having a hard time with this one -- can you help me?)
In the end, I drew the transformation myself, in a way that I hope will help you understand the use of the Reidemeister moves better:
- As you may be able to tell by now, I sometimes just like to have
fun with knots!
We've already started today with a little "knot equivalence" practice. Here's another one: what kind of knot is it, and which of these tools could you use to convince me?
- Number of crossings,
- Reidemeister moves, and
- tricolorability

Question of the day:
- Mobius bands are a part of geometry, but relate to a special area
called "topology" -- the study of form and shape.
The Topologist's favorite riddle: What's the difference between a donut and a coffee cup?
Answer: There isn't any! (to a topologist....)
- What is a Mobius band?

- Let's make some!
- A mobius band is made from a regular band using only a single twist.
- By the way, did you know that there are two different
Mobius bands? They're mirror images of each other! (Symmetry, again....)
- Check yours against someone else's, and convince yourself that they're really different.
- Make one of each!
- Properties of a mobius band:
- A mobius band has only one side.
- A mobius band has only one edge.
- Cutting a band:
- What happens when you cut a mobius band "in half"? Let's check out a bug on a band....
- What if you cut it into "thirds"?
- Applications of Mobius bands:
- Conveyor belts
- Kazakhstan's National Library in Astana
- Recycling Topology
- The official recycling symbol is mobius, but over
time an alternative has crept in:
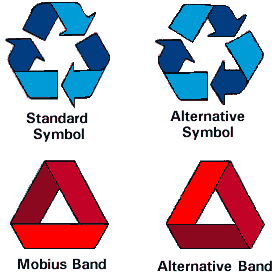
- My dad loved mobius bands so much....
- a history of the recycling symbol
- AARP article on the history of the creation of the recycling symbol
- Recycling -- Mobius, or only Seemingly Mobius?
- The official recycling symbol is mobius, but over
time an alternative has crept in:
- A joke: "Why did the chicken cross the Mobius band?"
- How does the Mobius band relate to knots and links?
- What kind of a knot is the edge of a Mobius band? (Cut one in half!)
- Do you get a knot with a twice-twisted Mobius band? (Cut one in half!)
- What objects (knots, links) did we get by cutting the Mobius band in "thirds"?
- What kind of a knot is the alternative recycling symbol shown above?