Day 33 in MAT229

Last time

Next time

Today:

Announcements:
- Your next exam is next Thursday, and will cover through 11.1.
- Your 10.4 homework is due...
- 10.3 Homework returned:
  - 4 -- notice that all the y-values are 1 -- so these three points are on a line.
    Nonetheless, you were supposed to use the polar coordinates to start. My point is this: after you do so, it's possible that your points don't all fall on a line. Refine your answer once you have more information.
  - 8 -- don't forget to cut out the boundary: ${0{\le}{r<2}}$
  - 28 -- Cartesian is easier for the displaced circle, whereas polar is easier for the circle at the origin. However, if you use the Cartesian coordinates for the first, you are better leaving the equation as an implicit function -- that is, don't solve for y (or, if you do, you must use plus/minus in your answer, to get both semicircles).
Review and continuation of Section 11.1: Sequences
- Let's start by taking a peek at p. 716, for review of the fundamental notion of convergence. It's a challenge....
- Definition: A sequence is a function f(n) whose domain is a subset of the integers. The values $a_n={f({n})}$ are called the terms of the sequence and n is called the index. For most of our sequences, the domain will be the natural numbers: {1, 2, 3, ....}.
- In the example sequence above, what do you suppose is the limit of the sequence as ${n \to {\infty}}$ ?
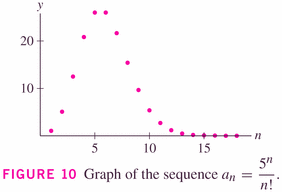
- There are lots of other sequences that we might encounter naturally: for example, there's one in probability and statistics that is closely related to the one we just looked at: the Poisson distribution, which has as its probabilities the sequence
  
  ${a_n=e^{-{\lambda}}\frac{{\lambda}^n}{{n!}}}$
  (what do you notice about the sum of the terms?).
- Other sequences might be defined in terms of a function. For example,
  
  ${a_n={\frac{1}{n}}=f(n)}$ where ${f(x)=\frac{1}{x}}$
  Examples:
  - #3, p. 724
  - #6
  Other sequences are defined by "recurrence" (e.g. the Fibonacci numbers)
  Example:
  - #12, p. 724
  Here's an especially interesting historical limit:
- One piece of good news: the obvious rules for limits are working:
  
  Examples:
  - #26, p. 724
  - #27
  - #29
- Some vocabulary: bounded sequences....
  
  And some theorems related to this notion:
  
  (especially useful for alternating sequences)
  
  (note that the converse is false)
  
  Let's use Theorem 6 to show that the sequence we initially considered is convergent:
- Geometric sequence: a sequence of the form
  
  ${a_n=c{r^n}}$
  where r is called the common ratio.
- Examples:
  - #23, p. 724
  - #67
  - #80
Section 11.2: Series
- A series joke:
  An infinite number of mathematicians walk into a bar. The first one orders a beer. The second orders half a beer. The third order a quarter of a beer. The fourth orders an eighth, and so on.
  The bartender says "You're all idiots", and pours two beers.
- Once we have some series in hand, we might want to start operating with them. In particular, as we saw in our very first series, we might want to add up the terms:
  
  We should get
  ${\sum_{n=0}^{\infty}\frac{5^n}{n!}={e^5{\approx} 148.4}}$
  Such a sum is called an infinite series.
- The question which presents itself is this: what do we mean by this sum of an infinite number of terms? This is indeed curious.
- Here's how we make sense of that infinite sum:
  - From the sequence ${\{a_n=\frac{5^n}{n!}\}}$
    we define a new sequence ${\{s_k\}}$ :
    ${\{s_k=\sum_{n=0}^{k}a_n=\sum_{n=0}^{k}\frac{5^n}{n!}\}}$
    These are called partial sums. Notice that there are two indices running around, and that the limit refers to the summation's upper limit, not to the index of the sequence.
    If
    
    ${\lim_{k \to \infty}s_k={\lim_{k \to \infty}\sum_{n=0}^{k}\frac{5^n}{n!}=L}$
    Then we say that
    ${\sum_{n=0}^{\infty}\frac{5^n}{n!}}$
    exists, and is equal to ${L={e^5}}$ . This justifies our probability distributions of the form
    
    ${a_n={e^{-\lambda}\frac{\lambda^n}{n!}}}$
    Because, in general,
    
    ${e^{x}={\sum_{n=0}^\infty\frac{x^n}{n!}}={1+x+{\frac{x^2}{2!}}+{\frac{x^3}{3!}}+...}}$
    This is an astonishing fact: we can think of an exponential function as a polynomial with an infinite number of terms. In fact, we can think of lots of functions this way (e.g. sines and cosines!). This is where we're headed in this class....
    More formally,
    
    Now geometric series are sufficiently important that it's useful to include that special case:
    
    There's a really fun proof of the first part above, based on a trick. Let's have a look at it.
    
    This theorem tells us that if a sequence isn't asymptotic to the x-axis, we can forget about its partial sums converging.
    Finally, series behave the way we'd hope:
  - Examples:
    - The harmonic series (Example 8, p. 732)
    - #1, p. 735
    - #2
    - #4
    - #15
    - #17
    - #61
    - #87
    - Beautiful spiral "proofs" of some infinite series

Website maintained by Andy Long. Comments appreciated.
Updated on 09/30/2014 23:35:07