- Your knot homework is due.
Today's
I'll start with the bonus: what do you think?
What questions do you have? Here's our work from last time, turning the unknot into a more interesting projection using Reidemeister moves, and then back again.
- What we learned last time is that, if the
projection of one knot is tricolorable and the
other isn't, they're different knots (because
we can't get from one to the other via
Reidemeister moves).
- Theorem: there are at least two different knots.
- The unknot is not tricolorable ("At least two colors must be used");
- The trefoil knot is tricolorable:

- The figure-eight knot is not tricolorable (it requires four colors):

- Danger: many knots are tricolorable --
being tricolorable doesn't mean that your knot
is the trefoil knot -- but it does mean that
your knot is not the unknot!
Links can be tricolorable, too -- for example, the unlink is tricolorable! (That's just two circles, one lying on top of the other, as in Borromean rings.)
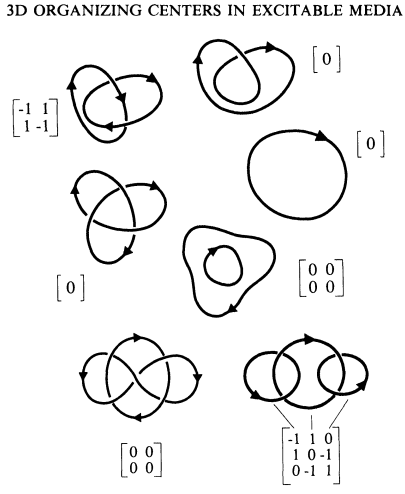
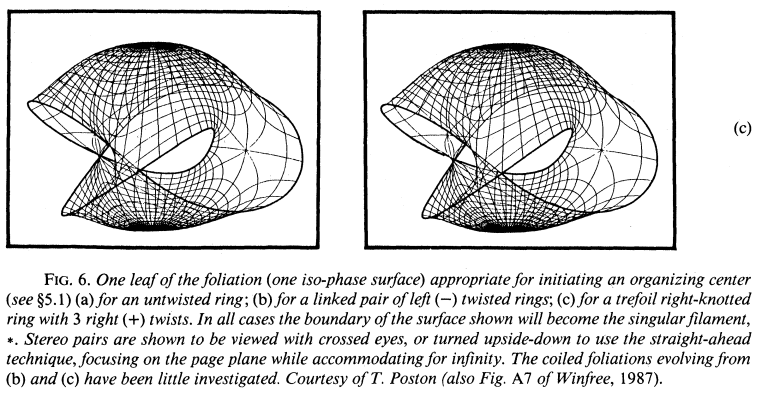
- Trefoil knots are in your heart
(the following images are from a paper by Art Winfree at the University
of Arizona, on "excitable media"):
-
- My dad carved mathematical objects, including this surface for Art Winfree (related to heart arrhythmias):
Hermann Weyl (German Mathematician; 1885 - 1955)
- I begin by using this
worthy handout, two pages of which I'll distribute today.
It covers two kinds of symmetry that are very important: rotational and reflective.
Your homework: to do the problems on the first three pages of this symmetry handout. This is due on Tuesday, 10/20.
- Are humans symmetric? Turns out that we're purported to have a "good side" and an "evil side"!
- We've seen symmetry in this course already: for example,
we noticed that in making our torus knots, we do the same thing at
every crossing point: the knot that results is rotationally symmetric.
Let's check that with the trefoil knot. Draw one, as a torus knot. Does yours look rotationally symmetric? What is a perfect projection's order of rotational symmetry (see your handout)?
(That is, we can draw it so that it has no rotational symmetry -- but that's our fault!)
- Another kind of symmetry is reflective symmetry.
- Can you draw another trefoil knot next to your first one, that is its reflection across a line?
- A figure-eight knot is equivalent to its mirror
reflection, which one can show by
Reidemeister moves. However the trefoil knot is
not equivalent to its mirror reflection.
- Reflective symmetric is relative to some line -- a line of symmetry.
- In the plane of 2-Dimensions,
- What is the most symmetric rectangle?
- What are regular polygons?
- How many regular polygons are there?
- What kinds of symmetry do they possess?
- Which regular polygons can be used to tile the plane?