- You have a homework due.
Question of the Day:
I have to say that I enjoyed our very spirited discussion of trees last time, and forests, and junkyards.
- Exercise: Let's see if we can show that the complete graph
with five vertices is not planar:
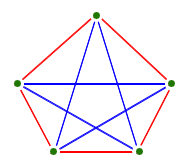
- We can show that the complete graph with four vertices is planar.
- Why not? What happens?
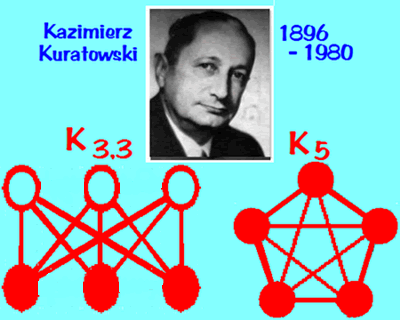
- The three utilities and three houses graph is not planar:

- Any non-planar graph has a copy of one of these two graphs
in it somewhere, as a subgraph:
- For Facebook, there is a difference between vertices: vertices are
labelled (with your name, perhaps. Pascal's triangle gives all
the ways of having a "Facebook" on any number of vertices. That's one
way that you can think about the rows of Pascal's triangle.
- One focus of this reading is negative numbers. It
was the Indians (of Asia) who put negative numbers on a
firm foundation (as well as zero), in about the 6th
century AD.
"...you can't see negative 4 cookies and you certainly can't eat them -- but you can think about them...." ("and you have to", says our author).
- One of the confusing aspects of negative numbers
from Strogatz's perspective is that the product of two
negative numbers is a positive number.
- But then Strogatz goes on to use the context of
social interactions (negative and positive) to discuss
how we maintain stable relationships.
And the key to understanding stability in three-way social relationships is that the product of two interactions (signified by either +1 or -1) must be equal to the other: so that if two legs are positive, the third in the triangle must be positive; if one leg positive, and the other negative, then the third leg must be negative as well.
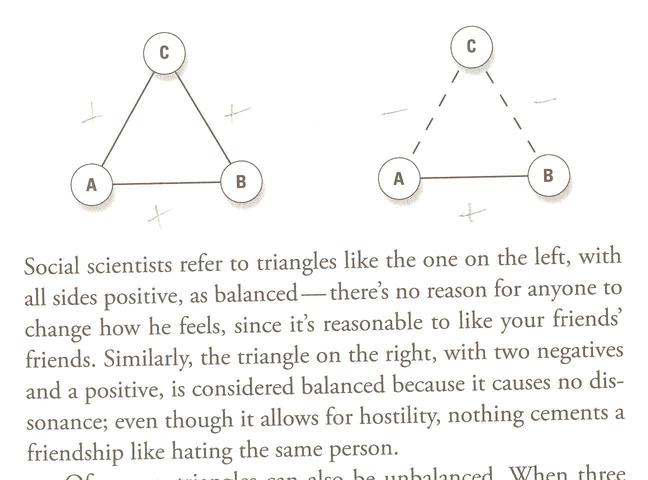
Strogatz sums up the second case above in the familiar saying that "The enemy of my enemy is my friend".
The following (two) graphs are unbalanced:
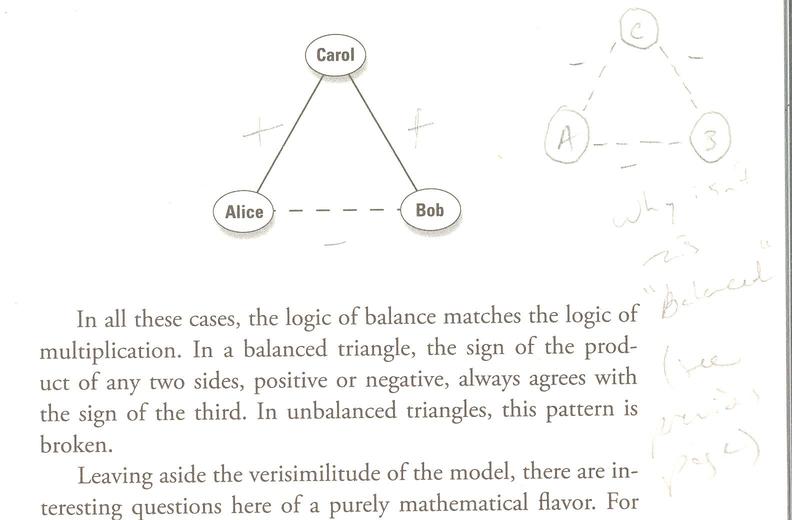
Finally Strogatz shows how historical relationships settled down into this pattern of stability: in "...the run-up to World War I. The diagram that follows shows the shifting alliances among Great Britain, France, Russia, Italy, Germany, and Austria-Hungary between 1872 and 1907."
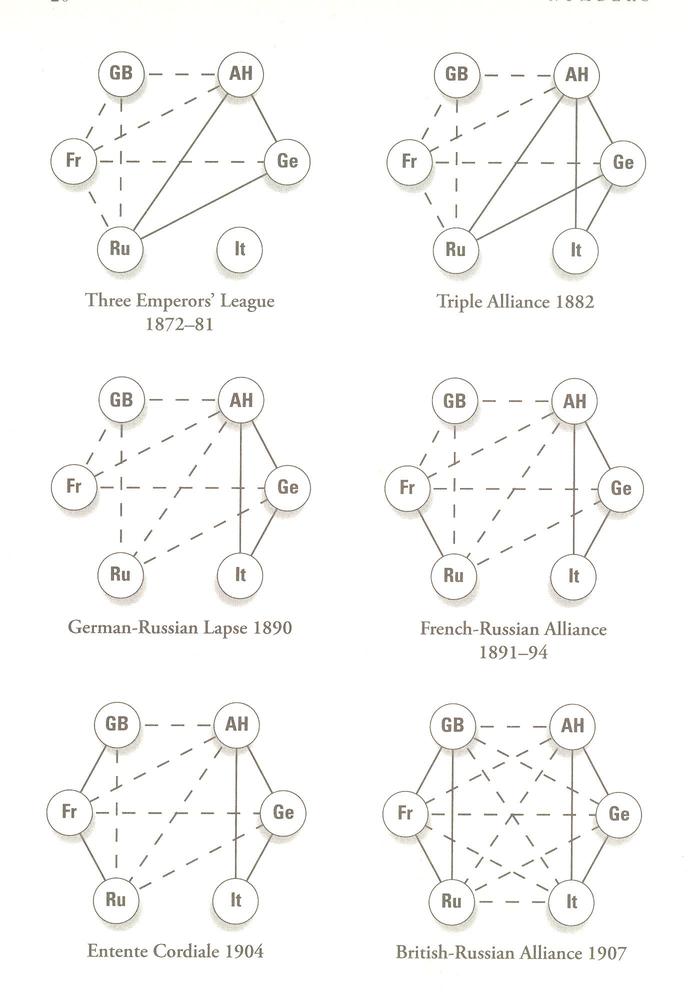
The bottom right graph (complete!) is the only stable configuration, "...balanced, but on the brink of war."
How do we know that it's non-planar?
This section describes how Google uses the "PageRank" algorithm to determine the importance of a webpage (and hence where it falls in the search results for a particular topic).
Graphs provide a useful way of illustrating how pages interact. If there's a link between two pages, then a directed arrow indicates it. Here's the graph of the "toy web" Strogatz considers, with the final rankings:
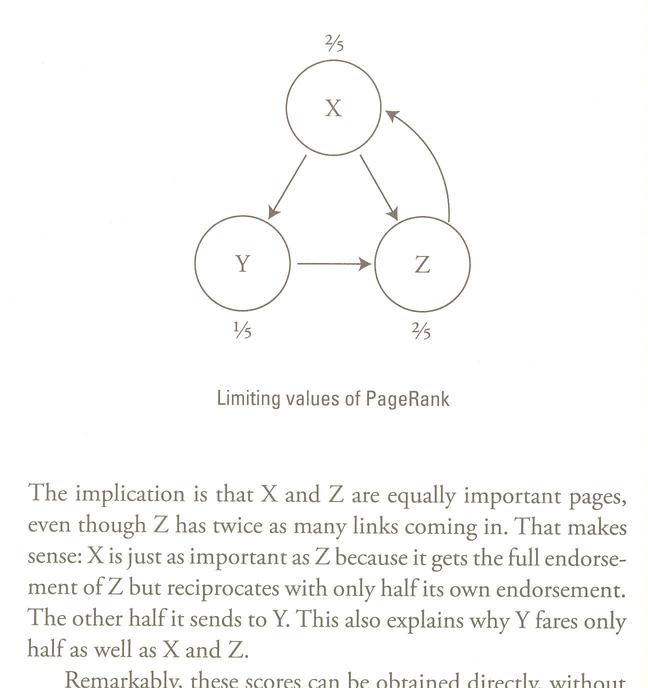
He justifies this ranking in a series of graphs, and a set of equations on page 195. Let's see how these equations work (we'll use this Excel spreadsheet).
Notice that I've written the equations with an index, ,
rather than with the primes. That's because we keep updating
the values to get them at the
stage, and we update based on the previous stage's (
)
values.
We just "do it again", over and over....
This strange algebra is from the field of mathematics called "linear algebra".
In this reading, we discover how to rotate and flip our mattress over the course of the year, so that the mattress gets even wear (while avoiding having to flip the mattress end-over-end the long way -- the "death-defying vertical flip").
"Spin in the spring, flip in the fall" is what some manufacturers suggest.
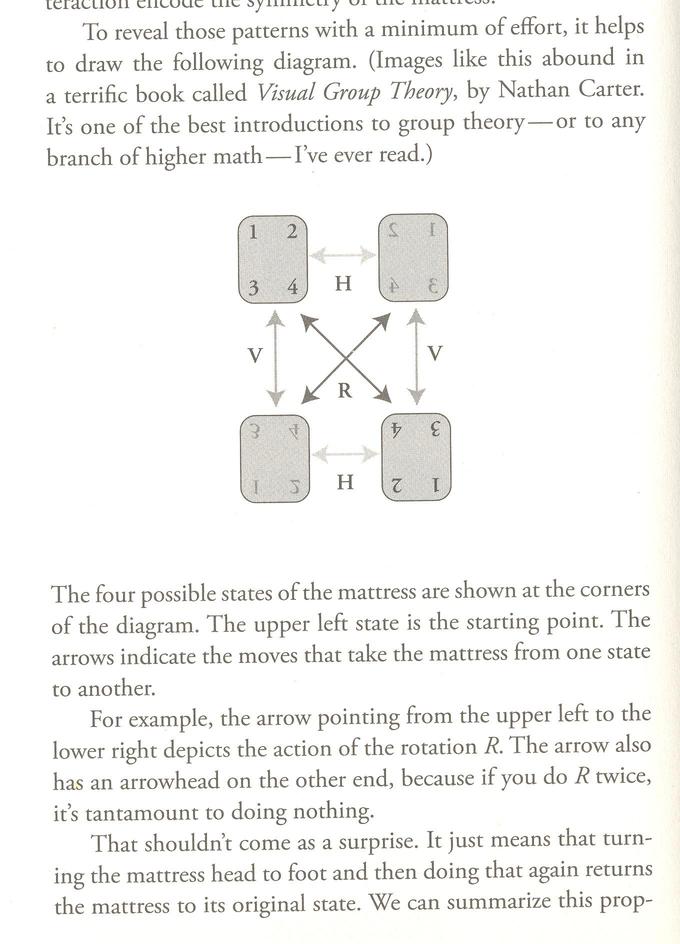
There is a certain amount of curious algebra here:
means that a horizontal flip followed by a rotation is equivalent to a vertical flip. Using only horizontal flips and rotations, we can achieve each of the four possible configurations of a matress. So over the course of two years, you'll have visited all four configurations of your mattress. Bon Nuit!