- Your exams are returned.
- Add 5 pts to your raw score; then your score is the percentage.
- There is a key.
- Fibonacci spirals
- The golden rectangle (and ratio)
- Now: what kind of rectangle will you get if you repeat the
spiral process with a non-Fibonacci rectangle to start (rather
than a 1x1 square)?
Turns out, that if you do it over and over and over again, you'll get a rectangle that gets more and more golden.
Let's try: we'll use a piece of grid paper (looking short and squat), and a 3x1 rectangle (start it running the tall-way at the 8th column, 12th row.
Now, are the ratios looking golden?
- The A0
Paper Fractal
"A paper" is something you've no doubt encountered before: it's the long sheets we occasionally use (usually "A4" paper), which is far more common in Europe.
"A paper" is constructed so that, if folded in half (do we say the long way or the short way?), you get a sheet which has exactly the same shape -- that is, the ratio of its side lengths is the same as the original sheet.
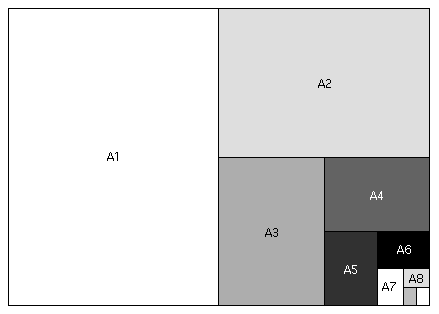
Let's see what the dimensions of A paper must be so that this requirement is fulfilled....
Call the long dimension of the A1 paper above
, and the short dimension 1.
- Then what are the dimensions of the A2 paper, according to the design of A paper?
- What is the value of
?
- Why not an A0 paper spiral? Let's try that....
This is the spiral, created using non-squares each time:
In both cases there's "the world within the world". Both are fractals.
- Fractals
- The concept of fractals is the most modern mathematics that we'll
study. We've worked our way up from the Babylonians all the way to the
21st century.
- This will be our intuitive definition of a Fractal:
-
A world within a world!
This key notion is more formally called "self-similarity": "a self-similar object is exactly or approximately similar to a part of itself (i.e. the whole has the same shape as one or more of the parts)."
- Some examples you have seen before:
- Our Fibonacci spirals
- Dual Platonics: e.g. a tetrahedron within a tetrahedron within a tetrahedron.... Maybe cooler are the other pairs, where we alternate solids (cube then octa), then repeat the process.
- The tree diagram of the rabbit problem that gave rise to the Fibonacci numbers.
- Often these arose out of the idea that we carry out a process, then "do it again, do it again"....
- Some examples you might have seen before:
- Here's a suitable mascot for this unit: Bessie the fractal cow:

- World's
Most Famous Fractal (Benoit
Mandelbrot, Novel Mathematician, Dies at 85: 10/14/2010):

- Here's a suitable mascot for this unit: Bessie the fractal cow:
- So what is a fractal? A
couple of things we'll generally see:
- It's a process or graph that possesses "self-similarity".
- It often possesses a simple and recursive (or iterative)
definition -- that is, we do something, and then we "do
it again!"
- Let's check out a beautiful gallery of natural
fractals.
It turns out that nature loves fractals, just like it loves Fibonacci numbers.
- Building deterministic fractals with sticks
- Consider the famous "Koch" fractal:
- Start with a straight stick.
- Replace the middle third of the stick with a little "tent" -- two third-length sticks.
- Do it again and again!
This fractal becomes infinitely long, but in a confined space! Very strange.... but this type of strange behavior is typical of fractals.
Let's make a variation of that. Use your graph paper, and a stick along the edge that's 27 units long. Best to use a pencil with a good eraser!
Intstead of triangular tents, we'll make square tents.
- Here
are some more lovely examples (including the Koch
fractal, but check out the beautiful bushes!).
- The Sierpinski triangle is an area fractal.
- Triangular paper is good for Sierpinski....
- First deterministically:
- After we're finished removing all that stuff, how much area is left in the triangle?
- Consider the famous "Koch" fractal:
- Now let's introduce a little bit of randomness: Sierpinski's
triangle again
The Chaos game - generating fractals using random movement!
- Once again, simple rules lead to complex
objects. This time, however, we don't proceed
methodically, but rather haphazardly - and yet we still
produce the complex images!
Here's a better version of that, that has more general options.
From randomness comes order; from simple rules comes complicated objects! Then all hell broke loose....
- Once again, simple rules lead to complex
objects. This time, however, we don't proceed
methodically, but rather haphazardly - and yet we still
produce the complex images!
- Deterministic
fractals: delve into an infinite, dynamic world, created by
a simple mathematical process:
- a simple rule
- repeated over and over and over.... but
- simple rules, intense content!
- The concept of fractals is the most modern mathematics that we'll
study. We've worked our way up from the Babylonians all the way to the
21st century.
- L-System Based Fractals (and a local copy).