Day 02, MAT115

As you prepare to do this homework, let's talk about some "lessons for life":

1. Keep an open mind.
2. Just do it. Jump in. Make mistakes and fail, but never give up.
3. Often when we've done it once, we do it again. Follow up one good deed with another!
4. Understand simple things deeply.
5. Break a difficult problem into easier ones.
6. Look for patterns and similarities.
7. Explore the consequences of new ideas. Generalize.
8. Examine issues from several points of view.
   Don't be a turkey -- be a dog! (this one may require a little explanation....)

Remember our "Question of the day" from last time:

How much would you bet against me? Would you make a smart bet?

So we might start by taking a look at that first reading, on Probability, to see what lessons the author (Tony Crilly) wants us to learn:

• Idea #31, a (a little history)
• Idea #31, b (ground rules)

• What's the probability that a die comes up 5? 6? 5 or 6? (This type of question is the focus of your first reading.)

• Big Ideas:

  1. Generally, if the situation is "fair" (meaning that all outcomes have the same chance of happening), then the calculation of a probability comes down to counting: if you can count, you can calculate probabilities.

     So let's think about the dice example described in the reading: we throw two fair dice, and then we might try to calculate the probability of "crapping out" in the game called craps:

     One "event" (crapping out) is given by throwing out either a 2, 3, or a 12.

     The set of all possible outcomes is called the universe of the experiment, or sample space. We often draw a picture to help us do our calculations, showing the universe, as well as those events that are "desired".

     Here's the universe of possibilities (sorted nicely so that you can see some of the sums that we need to count):

     

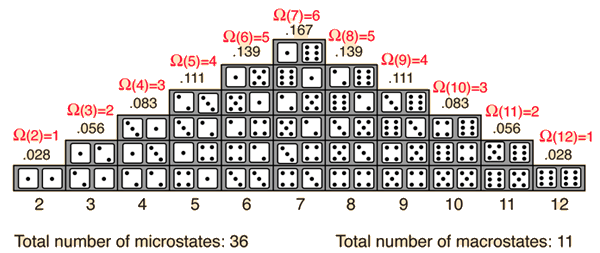
     In this picture, the outcomes ("microstates") are 36 in total number. What these folks call "macrostates" are the sums (and there are only 11 -- sums of 2 through 12).

     In general then, we compute the probability of an event by counting:

     

     We might write this in shorthand as

     

     where

     • E - is the event whose probability we wish to calculate
     • N - is the Number of outcomes that result in the event
     • T - is the Total number of outcomes possible

  2. Probabilities are numbers between 0 and 1.
  3. The probability of an event that is certain is 1.
  4. The probability of an impossible event is 0.
  5. The sum of the probabilities of each separate outcome possible is 1.
  6. When events cannot coincide, their probabilities can be added.

     So in the case of crapping out, we can write that

     

     where E is the event "crapping out".

     Now, if we use the counting principle, then

     

     and

     
     

     and

     

     So it checks out:

     

  7. One special situation in which "occurrences cannot coincide" is where we break the universe into two pieces which we might call event E and event "not E". So, for example, you might consider "crapping out" and then "not crapping out". These two events cannot coincide.

     If E is "crapping out", then we denote "not crapping out" by ("E bar").

     These are called complementary events, because they are non-overlapping, and every outcome falls into one event or the other.

     What we have learned, then, is that for complementary events one or the other must happen, but not both.

     So the sum of the probabilities of the complementary events must be 1 (the probability of certainty, since one or the other must occur):

     
     So the probability of "not crapping out" is
     

1. Assuming a fair six-sided die, let's calculate the probabilities of three events on a given roll:
   1. that a die comes up 5
   2. that a die comes up either 5 or 6
   3. that a die comes up odd

   Here's a strategy:

   • Draw the universe.
   • In each case, find those events that are desired.
   • Calculate the probability of the desired outcome.

2. Let's look at another problem: what's the probability of tossing a fair coin three times and getting exactly two heads?

   We'll use a tree to create the universe. [We'll find trees very useful throughout the course, and we'll actually be studying them later as graphs.]

3. It's not always easy to figure out the theoretical probabilities (as we did in the last two examples).

   What's the probability that an 81-year-old female in Wood County, Ohio will survive another year?

   That's the kind of question an insurance adjuster is concerned about, as am I: that's my mom!

   An approximation can be obtained by looking at records for Wood County for the last year and counting those who survived versus the total number of such women:

   

4. Your reading introduced another way to represent the universe of possible outcomes in the game of craps. We're able to use a table to compute the probability of a 7 or 11 (a "natural" in craps):

   1 2 3 4 5 6 1 (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) 2 (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) 3 (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) 4 (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) 5 (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) 6 (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)

   The sample space or universe for a roll of two dice.

   Let's do a few more calculations:

   1. 
   2. 
   Now that we've calculated those, here are some easier ones:
   1. 
   2. 
   Since these events are complementary events, we can compute the probability of a complementary event by doing a simple subtraction from 1:
   

I want to bet on the event "two (or more) people in the room have a common birthday".

How much would you have bet against me? Would you have made a smart bet?

Now we're going to use a strategy that we've introduced today: it turns out to be easier to compute the complement of the event, which is the probability that all students in the room have different birthdays. Let's count. How many possible birthdays? Let's suppose there are 35 people in the room.

What about leap years? Forget 'em! (Mathematicians often simplify a problem to make it easier to deal with.)

1. First, the universe: how many different birthday combinations are possible?
   

   That's because each person chooses one of 365 different birthdays, and each person chooses independently of all the others. So we multiply

   

   (35 times).

2. Now how many birthday combinations give rise to the event (no common birthdays)?

   

3. We're ready to calculate the probability of :

   

   Calculating that out, we get

   

   Now that's the probability that my opponent will win: the probability that I will win the bet is the complement, i.e.

   

Let's say "Bobby" is going to play against me. How much should Bobby bet against my $10 (so that the bet is "fair" in the sense that if you play over and over, on average you break even)?

Let's say we play this games 100 times (in 100 classes).

Based on the probabilities, I would have been right about 81 times out of the 100. So if I bet $81 dollars, and Bobby would have bet $19, then over the long term I'd pay to Bobby, on average,

If I bet $10, then Bobby would have bet 19/81 of that: $2.35

• The rules:
  1. There are three doors, behind which are two donkeys and a car.
  2. You choose one: Monty Hall then shows you a door behind which appears a donkey, then offers you the chance to either "stick" with the door you chose at first, or "switch" for the third door.

• The question: Do you stick or switch? How can we decide?

  Marilyn vos Savant said "Switch!" -- and she's the smartest person on the planet, right?

• The analysis: We should be able to do this theoretically:

  • What's the sample space?

  • What's your probability of success given that you stick? What's your probability of success given that you switch?

    Sticking and switching are complementary strategies. One strategy will win, and one strategy will lose. Hence,

    P(win by sticking)+P(win by switching)=1

    from which we conclude

    P(win by sticking)=1-P(win by switching)

  • The easy one to calculate is the probability of winning by sticking: 1/3. Hence, switching is better by twice, 2/3!

• Let's check our answer: we might simulate the game.

  Let's break into groups to play, and see if our theoretical answer is correct:

  • Three cards represent the three doors; choose one card to be the "car", and the other two cards to be donkeys.
  • Try 10 (or more) plays where one player always sticks and the other always switches.
  • Tally up the successes of each strategy (realizing that if sticking wins, switching would have lost, and vice versa -- the events are complementary).
  • Is one strategy better? If so, by how much? "What are the odds?"
  • Then we'll combine the class's data, to "see what the data says".
  • Now: Can you justify/explain your answer?

• Is it possible that by restricting the game, or by extending the game, we might learn more?

  To give you more confidence in the answer (and perhaps to learn more!), we may consider extending the game: what if we have ten doors, one car, and nine donkeys. After you pick your door, Monty shows you eight doors with donkeys behind them. Would you switch for the remaining door? How much better is one strategy over the other?

You rub an old oil lamp and a genie appears. You ask for a wish - since you let him out of the lamp, after all. Reluctantly the genie agrees. You tell him you want the Royal Black Diamond - a famous gem worth millions of dollars. At your feet appear 27 identical - looking gems. You ask Mr Genie what is going on and he replies that you may take any one of the stones with you. They are identical in appearance, but the genie explains that the Royal Black is slightly heavier than the 26 fakes. At this you say, " Great I wish I had a way to weigh them!" The genie grants your wish and a magic balance scale appears at your feet. The genie explains that upon being used three times the scale will disappear. Can you find a way to choose the right gem from the 27?

With 8 stones we could put half on one side and half on the other and the heavier side will contain the RBD. Repeating this twice will leave us with the heaviest stone after 3 uses of the scale. Now how do we adapt this idea to 27 stones?

We could put some, say 10 gems on one side, 10 gems on the other side, and leave 7 off the scale. If one side of the scale is heavier, then it must contain the RBD. If neither side is heavier, then the RBD is among the 7 left off the scale. So we can learn about gems not on the scale! But we need to divide the gems up more carefully....