Day 21, MAT115

We start with a so-called "Fibonacci spiral" (see this site) and move to the golden rectangle (which is fractal by definition).

With your graph paper in the short and squat position (wider than tall), color in the square in the 10th column and the 6th row.

From there we'll spiral out in the counter-clockwise sense. At each step we will append the largest square possible to the existing rectangle (and we'll see a link to the Fibonacci numbers).

• "The Sexiest Rectangle" - or is it just cute?
  • Important property, which defines the rectangle:
    A rectangle is golden if, when you cut out the largest square possible, the rectangle remaining is still golden!

    This is the fractal nature of the golden rectangle: there's a perfect copy of "the world within the world" in the golden rectangle....

  • The golden mean (or golden ratio, golden section) -- A "precious jewel" (Johannes Kepler)
    • derived by ratios of Fibonacci numbers, or
    • using the rectangle directly. The Greeks defined a golden rectangle by calling it the rectangle which, when the largest square possible is removed, retains its shape (which means that the ratio of side lengths doesn't change).
    • The golden rectangle has side lengths in the ratio

      Note that the value is only approximately 1.618: is an irrational number, like , and its decimal representation goes on forever and never repeats:

      

• Now: what kind of rectangle will you get if you repeat the spiral process with a non-Fibonacci rectangle to start (rather than a 1x1 square)?

  Turns out, that if you do it over and over and over again, you'll get a rectangle that gets more and more golden.

  Let's try: we'll use a piece of grid paper (looking short and squat), and a 3x1 rectangle (start it running the squat-way at the 12th row, 8th column

  Now, are the ratios looking golden?

• The A0 Paper Fractal

  "A paper" is something you've no doubt encountered before: it's the long sheets we occasionly use (usually "A4" paper), which is far more common in Europe.

  "A paper" is constructed so that, if folded in half (do we say the long way or the short way?), you get a sheet which has exactly the same shape -- that is, the ratio of its side lengths is the same as the original sheet.

  

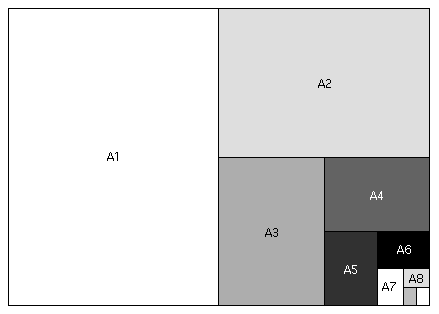
  Let's see what the dimensions of A paper must be so that this requirement is fulfilled....

  Call the long dimension of the A1 paper above , and the short dimension 1.

  • Then what are the dimensions of the A2 paper, according to the design of A paper?
  • What is the value of ?

• Why not an A0 paper spiral? Let's try that.... This is the spiral, created using non-squares each time:
  

  In both cases there's "the world within the world". Both are fractals.