- Your next assignment is due Monday.
- On the horizon: our next exam is next week, Friday, 4/10.
- We went over the homework, and, in particular, talked about how
some fractals are infinite in length in a finite amount of space. If
something is doubling at every step, and the steps go on forever, then that
"something" is heading for infinity. So if the length doubles at each
step, it will become infinitely long "in the end".
Doubling at every step (or increasing by a factor of four at every step, etc.) is an example of exponential growth, which is generally considered to be very fast growth.
- We practiced creating fractals.
- Graphs don't change by bending edges, but breaking them or
detaching edges from their vertices (and hence creating new vertices)
gives new graphs.
- A graph is simple if it doesn't have any loops (edges connected
from a vertix to itself), or multiple edges with the same two vertices.
Now: how might we relate this concept to Facebook?
- Previously we drew all the simple graphs with one, two, and three
vertices.
For these graphs we imagine ignoring the differences between people. All vertices are considered the same.
So these represent common social situations, without regard for which individuals are being affected.
- Let's review the simple graphs with four vertices.
- Have you ever seen any of these before? Could we give any of them names?
- Planar graphs are graphs that can be drawn such that no two edges
intersect.
- Complete graphs are simply graphs with connections between
every pair of vertices (but no loops).
- Exercise: Let's show that the complete graph with five
vertices is not planar:
- We can show that the complete graph with four vertices is planar.
- Why isn't the five graph planar? What happens?
- The three utilities and three houses graph is not planar, either:
- Any non-planar graph has a copy of one of these two graphs
in it somewhere, as a subgraph:
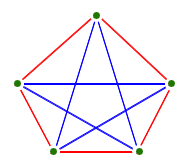
- Chapter 3: The Enemy of My Enemy (complete graphs)
- The focus of this reading is negative numbers. The
Indians (of Asia!) also put negative numbers on a firm
foundation (as well as zero), in about the 6th century
AD.
"...you can't see negative 4 cookies and you certainly can't eat them -- but you can think about them...." ("and you have to", says our author! p. 15).
- One of the confusing aspects of negative numbers
from Strogatz's perspective is that the product of two
negative numbers is a positive number. The story about
the two linguists is priceless (p. 17).
- But then Strogatz goes on to use the context of
social interactions (negative and positive) to discuss
how we maintain stable relationships.
And the key to understanding stability in three-way social relationships is that the product of two interactions (signified by either +1 or -1) must be "equal" to the other interaction: so that if two legs are positive, the third in the triangle must be positive; if one leg positive, and the other negative, then the third leg must be negative as well.
Furthermore, if two interactions are negative, then the third must be positive -- (-1)(-1)=(+1) -- a negative times a negative equals a positive.
Strogatz sums up the second case above in the familiar saying that "The enemy of my enemy is my friend".
The following (two) graphs are unbalanced:
Finally Strogatz shows how historical relationships settled down into this pattern of stability: in "...the run-up to World War I. The diagram that follows shows the shifting alliances among Great Britain, France, Russia, Italy, Germany, and Austria-Hungary between 1872 and 1907."
The bottom right graph (complete!) is the only stable configuration, "...balanced, but on the brink of war."
- The focus of this reading is negative numbers. The
Indians (of Asia!) also put negative numbers on a firm
foundation (as well as zero), in about the 6th century
AD.