Day 05, Mat227

Last time

Next time

Announcements:
- Reminder: turn off your rectangles.
- Your first assignment is due today
  - Justen's #28
Section 4.2: The definite integral
- This section generalizes our intuition and examples from the preceding section.
  - There's a lot of notation. Try not to let that intimidate you. A lot of Greek letters. A lot of indices, like i. There are parameters floating around, like n.
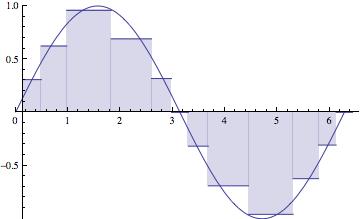
- Last time we got to a point at which we had a thing, called a "Riemann sum", based on the following stuff:
  - a function ${f}$ ;
  - an interval [a,b] over which to calculate the area;
  - a "partition" P of the interval into N subintervals, with "endpoints" ${x_i}$ and widths ${\Delta{x_i}}$ ;
    i is a variable (an index) that runs from 1 to N. It indicates the particular subinterval (the i^th subinterval) under consideration.
    So the endpoints of the i^th subinterval are ${x_{i-1}}$ on the left, and ${x_i}$ on the right.
  - A set C of "Centers" ${c_i}$ of the subintervals, at which we calculate the function values ${f(c_i)}$
    "Centers" might be a poor choice of words, since the centers may not be at all in the centers of the subintervals.
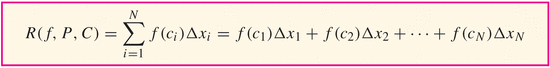
  From this stuff we construct the appropriate sum:
  
  where P is a partition of the interval [a,b]:
  ${a=x_0<x_1<x_2< \ldots < x_N=b}$
  and where C is a set of centers,
  
  ${C=\{c_1,{\ldots},c_N}\}$
  such that each center falls in one subinterval, where i runs from 1 to N:
  
  ${c_i\in[x_{i-1},x_i]}$
  Last time we saw that a rectangle method dictates a choice of "centers" for the Riemann sum:
  - LRR: ${c_i=x_{i-1}}$
  - RRR: ${c_i{=}{x_i}}$
  - MID: ${c_i{=}{\frac{{x_i+x_{i-1}}}{2}}}$
    (this one really is in the center of the subinterval -- that's the average of the two endpoints).
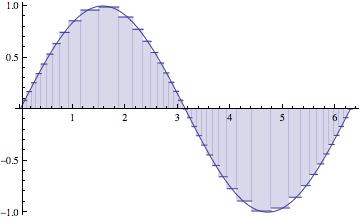
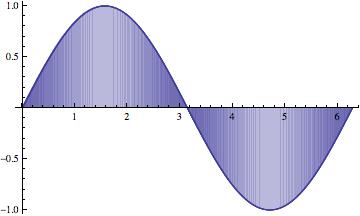
- If the size of the intervals goes to zero, then the approximations get better and better, until they're perfect!
  
  where
  ${||{P}||}$ is the width of the largest subinterval, ${max(\{\Delta{x_i}|i\in\{1,\ldots,N\}\})}$ for the partition.
The maximum subinterval width ( ${||{P}||}$ ) goes to zero. The partition gets thinner and thinner, as the number of subintervals (n) goes to ${\infty}$ .
In particular, if ${f}$ is continous on [a,b], then ${f}$ is integrable.
If it's continuous except for a finite number of jump discontinuities, it's still integrable.
So lots of important functions are integrable.
Some Important Properties of the Definite Integral (there are more in your textbook!):
Here's how we'd rewrite our generalization that Area under the graph of f from a to b =

${{\bar{f}}(b-a)}$ ${\int_{a}^{b}f(x)dx=\bar{f}(b-a)}$ where by ${\bar{f}}$ we mean the average value of ${f}$ .
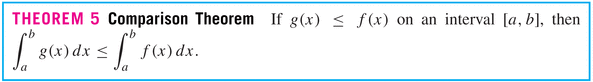
Again, we can use this relationship to define the average value of a function on the interval [a,b]
Examples:
- Linear and quadratic functions
- #10, p. 307
- #33
- #21

Website maintained by Andy Long. Comments appreciated.


The maximum subinterval width ( ${\|\|{P}\|\|}$ ) goes to zero. The partition gets thinner and thinner, as the number of subintervals (n) goes to ${\infty}$ .