Day 10, Mat227

where is any particular anti-derivative.

Our author does mention that a function is an anti-derivative of its rate-of-change: i.e.,

It looks different than the one above, but it says exactly the same thing, of course.

Important Example: We use this notion time and again in applications.

So, for example,

• the position of a particle is an anti-derivative of the velocity of the particle;
• the velocity of a particle is an anti-derivative of the acceleration of the particle.

In free-fall, a particle's acceration near to the earth is approximately constant (the acceleration due to gravity is ).

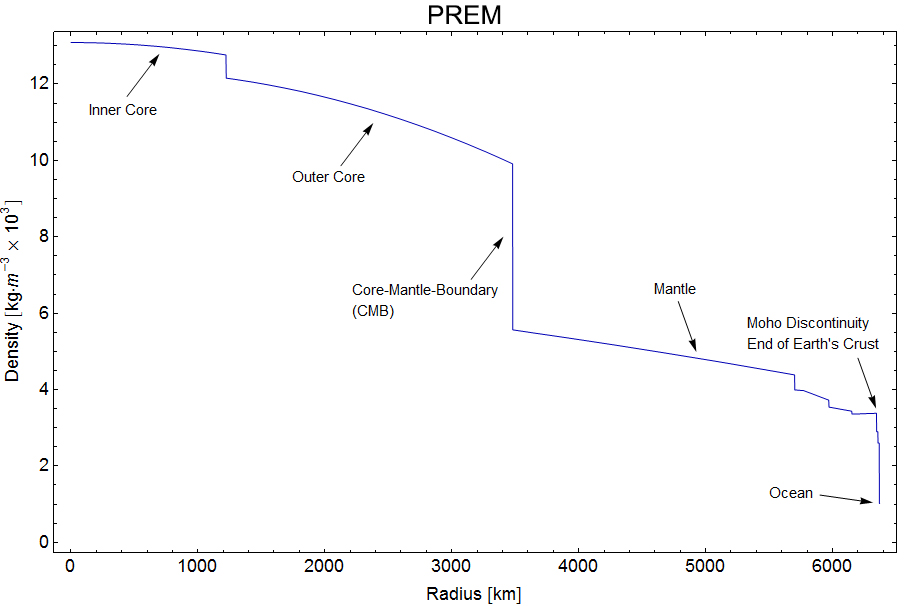
• Preliminary Reference Earth Model (PREM) Data
• I saw that graph and decided to calculate the mass of the Earth is the integral of the density:

Now, if the particle starts falling, with initial velocity (at ), then its velocity will be given by

or

or

(since the constant is known at ). (What are the units of velocity?)

Now we can calculate the position (initially at height ):

or

or

(What are the units of position?)

And that is what Newton was doing under the apple tree, when the apple fell on his head and he discovered the law of universal gravitation (and that the moon also could fall on his head, were he not lucky).

So, as mentioned in class, differentiation and integration are not quite inverse processes: the derivative of a function is unique, and an infinite number of functions have the same derivative; vice versa, a function has an infinite number of anti-derivatives.

• #1, p. 326
• #5
• #45
• #50; furthermore, what does
  

  represent?

• #63

• The substitution rule is the chain rule backwards. Every differentiation rule is written backwards to create an integration rule. Substitution is the flip side of the chain rule.
  • Q. What is the derivative of ?

  • A:

  • Hence,
    

  More generally:

  • Q. What is the derivative of ?

  • A:

  • Hence,
    

  That's the general idea. So, in terms of a definite integral, the rule is that

  and, even better in some minds, make a substitution of variable:

  We can always do the change of variables

  

  and hope that the integral on the right is easier to solve (certainly less cluttered). Notice especially the change in the limits on the integral.

  Writing it in this last way may be mysterious, because of the change of variable to u (and the change in the limits); but it's the disappearance of g'(x) that's really curious. It falls right out of the change of variables, however:

  Solving for du, we get and hence that piece of the integrand disappears.

• Examples:
  • #2, p. 335
  • #5
  • #8
  • #19
  • #38