- Your 4.5 homework is returned. Graded 16, 25, and 38. Pretty straightforward stuff.
- Your homework for 5.1 is due Monday.
You also have a homework for 5.2 due Wednesday, 3/4.
Before we leave, however, I need to issue a correction that Grant brought to my attention:
For my final example, I neglected to square a term (#5), so I want to fix that.
Then I'd like to revisit the computation of Earth's mass from last time, which I did via a method of "spherical shells". In that case we have a sphere, which has a mass density function
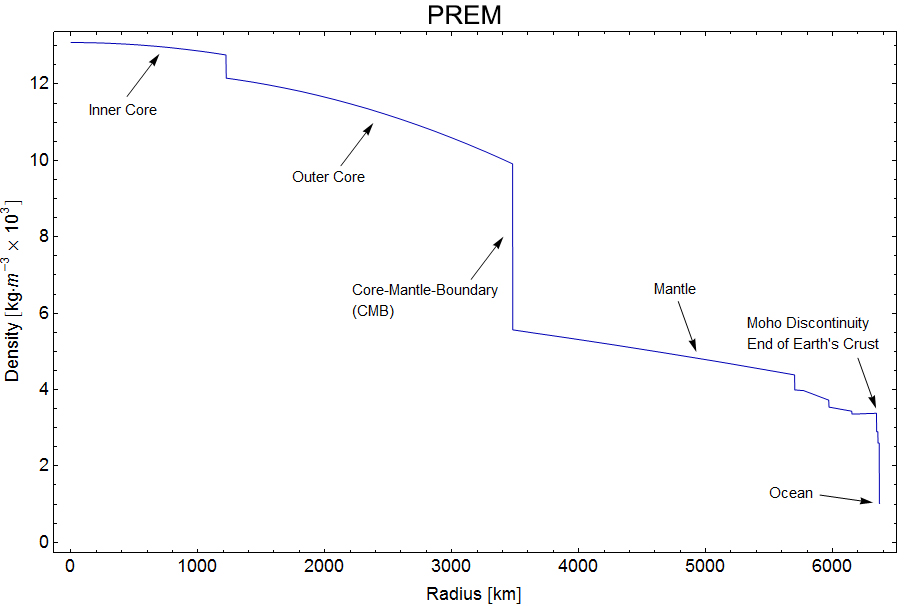
I saw that graph and decided to
The shells look like this (imagine an onion). At left is a "dV", a little chunk of volume. We'd multiply that dV times the mass density at that radius, to get a .

Then we add up the in an integral:
where is the radius of the Earth.
- While up in Canada recently, I had to convert between Fahrenheit
and Celsius. In particular, I was given a temperature in Celsius
(-20oC) and wanted to hear it in oF.
-
Activity 1: given a sheet of graph paper, the fact that the
relationship is linear, and using the two points
independent dependent oC oF 0 32 100 212 create a nice graph of
(Fahrenheit as a function of Celsius). Compute
.
Then write the linear function g that converts C to F.
As soon as we answer that question, we'll probably want to know: how do we convert between Celsius and Fahrenheit? That's the inverse function!
Write the linear function
that converts F to C.
-
Activity 2: given the graph of
, create the graph of the inverse function (
).
Now: would we want to carry out stage three of the three-step process of computing an inverse function? That is, would you want to exchange the variable names of the dependent and independent variables?
Now you made nice graphs: criticize my graphs in the Mathematica summary.
- Why study inverse functions (and inverse problems, more generally)?
- Pollution
- Forensics
- Ballistics
- Activity 3: Examine this figure:

- Is Temperature
an invertible function of altitude (
)? Why (or why not)?
- Is Atmospheric Mass Density
an invertible function of altitude (
)? Why (or why not)?
- What does the inverse function measure, if it exists? What questions can it answer?
- How can you explain those values for mass density along the y axis?
- Is Temperature
- Examples: Let's run the odd exercises from 3-15, p. 390.
- Now, let's look at a particular function:
- How do we compute
?
-
?
- Find a formula for
?
- How do we compute
- Now: is
invertible? How can we use
- properties of this class of function to help us answer this question?
- calculus to help us answer this question? (In particular, how we can use the derivative?)
- Let's derive the derivative of the inverse, using a neat trick:
the inverse identity
and the chain rule.
- Whether a function is invertible or not, one can propose to find the derivative of its inverse using this process. Use the process to find the derivative of the "inverse of sine" (although that clearly makes no sense at this point, since sine is not one-to-one).
- How about the derivative of the inverse of
?