- Your homework for 5.1 is returned. Graded 4, 13, 21.
- Use symmetry. It reduces work, so is smart.
- A very disheartening tale....
It starts with "Catastrophic errors". Dan McGee, Director of the Kentucky Center of Mathematics, gave me something useful today: the notion of the "catastrophic error", which he introduced to Puerto Rico.
Let me give you an example...
- You have a homework for 5.2 due today.
- Your 6.1 homework will be due the Monday after spring break.
- We were scheduled to have another exam on 3/20 to celebrate the arrival of spring -- we've agreed to push it back to 3/27.
- First of all, exponential functions have a characteristic shape:
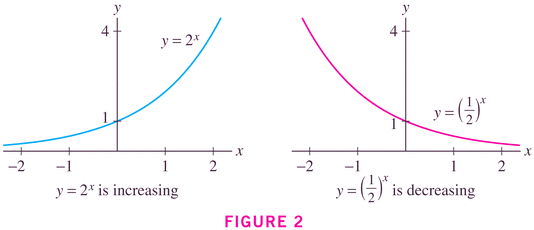
This pair of graph should remind of us two important concepts that you will have heard about in science classes at some point: doubling time, and half-life. How so?
- Exponential functions are useful in all kinds of applications: whenever the
rate of change of a function is proportional to the function itself,
you'll see exponential functions putting in appearances.
- Financial (bank accounts, loans, etc.)
- Biology (population growth)
- Forensics (Newton's Law of Cooling)
- Forest Modeling
How do we write that mathematically?
The concept is often misused in common parlance, however: you'll often hear someone say that something's "growing exponentially!" -- by which they mean what?
Do you think that this physical quantity (Total Global CO2 emissions) shows signs of exponential growth?

The data is represented by the blue graph -- what do you suppose the dashed graph represents?
Take a look at Figure 9, p. 395, in this section. Is the exponential doing a good job of fitting the data?
- Laws of Exponents:

Of course the negative exponents law causes us trouble when we talk about inverses of functions: may people will make the mistake of thinking that the inverse function
is the same as
because of this law. But it's not.
The real problem is that we mathematicians are too lazy: we keep reusing notation, even to the confusion of our students.... We need to be attentive, and interpret the notation in context. Mathematicians are not alone, however: the same is found in language, right? What is "lead"? Did I lead a squad to victory, or were we mowed down in a shower of lead?
- Shape as a function of base:
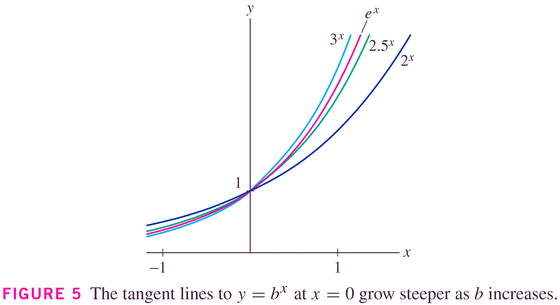
- Demonstration of the derivative property of exponential functions (that an
exponential function is its own derivative, up to a constant multiple).
- The following two properties are two sides of the same coin: but they're the most important reasons for the choice of the irrational base e:
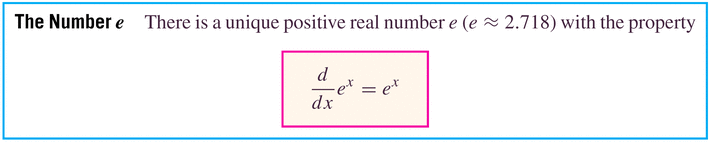
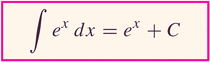
This is almost a magical property: the rate of change of an exponential function is proportional to its value. In one case, the rate of change is the function value. The slope of the tangent line is the value of the function. Curious!
- Examples:
- #13, p. 401 (review of translations, reflections, etc.,
using
)
- #17
- #36
- #13, p. 401 (review of translations, reflections, etc.,
using