- Your quiz is returned from last time.
- We did this one in class.
- Did you notice that the function in part 1 was similar to the negative of one of the functions in part 2?
- Use symmetry, powers of polynomials, location of zeros, inflection, etc.
- Derivative of tangent
- Fourth derivative of sine, cosine
- #7, p. 146
- #26
- #35
- #49 and 50
- The chain rule is so critically important because of the
importance of compositions of functions: for
$F(x) = f(g(x))$,
$F^\prime(x) = f^\prime(g(x))g^\prime(x)$ I personally think this to myself: "f prime of stuff times the derivative of the stuff"; or "f prime of stuff times stuff prime.",
where $f$ is the "outside" function:
$F^\prime(x) = f^\prime(stuff)stuff^\prime$ You can see that the rule is fairly simple, once you've identified the composition -- that is, once you've torn apart $F$ to find $f$ and $g$.
We took a look at a file from my pre-calc class to review compositions. Remember?
- The difficulty is often identifying the composition. We'll try
some easy ones first, then get to some ugly ones.
Before we do that, however, I'd like to show how to derive the chain rule, using the limit definition of the derivative. Everything comes from that! I'll need to use a result from p. 153, where the chain rule is proved in our text.
Basically, however, it relies on the tangent line: we want to use the fact that
$f(x+h) \approx f(x) + hf'(x)$ Why does that make sense? Because it comes straight out of the limit definition, where we throw away the limit. That's why we have to write "$\approx"$:
$f'(x) \approx \frac{f(x+h)-f(x)}{h}$ - #9, p. 154
- #16
- #29
- #42
- #77
- A Chain Rule tutorial
- A sample problem involving compositions: model the seasonal variation in Keeling's CO2 data:
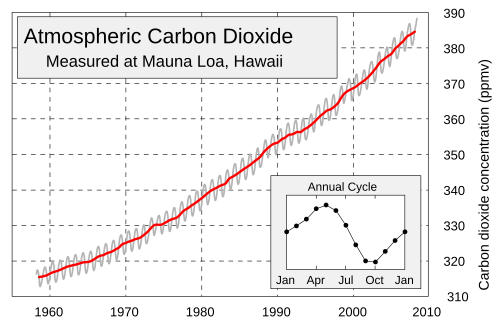
- Keeling data with models:
If time were measured in years from January, would
$V(t)=A\sin(2\pi{t})$ be a good model? What would be a good choice for the parameter $A$?