MAT115: Math for Liberal Arts

Homework:

1. Read the short on-line article "From Fish to Infinity" for next time.
2. Your extra-credit assignment, should you choose to accept it, concerns the card trick (The Ice Cream Trick) that we saw in class:
   1. Take about a quarter of a deck of cards.
   2. Ask the volunteer what kind of ice cream they like.
   3. Give them "a scoop" by
      1. counting out one card for each letter in the name of their ice cream;
      2. then covering with "toppings" (the rest of the cards dropped on top).

   4. Repeat two more times, for a total of three scoops.
   5. Magically tell them the card that's on top of their sundae. (By the way, there's always something that the magician isn't telling you....)
   Your mission:
   1. How does the trick work?
   2. Does it always work (for all flavors of ice cream)?
   3. What is the secret to success?
   Write up your answers and turn them in before class if you want credit.

   Of course you will ultimately try this on your friends, and astound and amaze them! Maybe you can win some money??

Homework (due Thursday, 1/21):

• There are some people on an elevator. Suppose you bet your buddy that two people on the elevator have a common birth day-of-the-week (I was born on Saturday -- do you know what day of the week you were born on?).
  1. How many people in the elevator would guarantee that you win?
  2. What's the fewest number of people on the elevator that would give you the advantage over your friend? You might create an experiment to test your guess, and report the results of your experiment....

• For the following use the method of "primitive counting" described in class (day 2):
  1. Turn the following into the appropriate string of 1s and 0s (drawing the tree for me is best):
     1. 32
     2. 63
     3. 97

  2. Turn the following strings of 1s and 0s into the appropriate number of sheep (again, drawing the tree for me is best):
     1. 101010
     2. 1010101
     3. 10110001

1. Write the following numbers in the Babylonian number system:
   1. 57
   2. 222
   3. 817
   4. 9432
   5. 14449

2. Translate the following tablet, and explain its purpose:
   

3. Extra credit: write a one-page story about the kid who created the Babylonian clay tablet nines table we studied, and about how the tablet ended up in our hands today. Complete fiction appreciated. (I'll post these, and we'll have a contest -- the winner(s) will win "get out of homework free cards" as well).

1. Write the following numbers in the Mayan number system:
   1. 57
   2. 222
   3. 817
   4. 7581
   5. 9432
   6. 79420
2. Complete your Mayan lunar calendar and hand it in. Please show some work for the calculations -- no work, little credit.

Homework (due Tue, 2/2):

Use Fraudini's trick to write the following numbers as sums of powers of 2 (you'll need some additional powers of 2):

1. 31
2. 57
3. 129
4. 222
5. 817

Homework, to turn in next Thursday, 2/4: on your handout,

1. Complete a version of the triangle using our numbers (i.e. translate this triangle), and
2. write the next row of Yanghui's triangle, using the notation of the bamboo counting rods. Use the patterns we discover in class to figure out what row comes next. This will be due next Tuesday. Include an explanation of how you chose to represent any numbers that haven't already appeared in the table.

Homework (for Tuesday, 2/9): first of all, a reading assignment: please continue reading your text to page 28.

Then hand in the following:

1. Suppose you are about to begin a game of Fibonacci nim. You start with 50 sticks. What's your first move?
2. Suppose you are about to begin a game of Fibonacci nim. You start with 100 sticks. What's your first move?
3. Suppose you are about to begin a game of Fibonacci nim. You start with 500 sticks. What's your first move?
4. Suppose you begin a game of 15 sticks by taking 2; your friend takes 4; what's your next move, that will lead to victory provided you know the strategy?

• First, a reading: please read pp. 121-139. I know that it's about algebra, but read it anyway! It's good for you....
• Measure 5 different rectangles around the house that look like they might be golden. Calculate their ratios, and see how close they come to being golden.
• Make a truly beautiful artistic Fibonacci spiral. For example you can do it graphically, by using square pictures of friends, family, landscapes, etc. of increasing size.

1. In how many different ways can you put 5 friends into 2 different vehicles for a trip to the graduation party, where 2 friends go in one car, and 3 friends go in the other?
2. In how many different ways can you put 5 friends into 2 different vehicles for a trip to the graduation party (assuming either car could take all)?
3. How many different ways can you choose 3 candy bars from 6 different candy bars?

Homework (due 3/1): Demonstrate Egyptian multiplication by multiplying (write out the table, and check your work):

• 13*34
• 23*79
• 81*123
• 255*256

Reading assignment: Please read pp. 28-31, 43 (biography of Pascal), and 48-59 for Tuesday.

Homework (due 3/3): Demonstrate Egyptian division in two ways:

• Demonstrate Egyptian division by dividing:
  • 9/4
  • 13/7
  Try these using the same sort of "doubling/halving" table that we use for multiplication.

• Demonstrate Egyptian division by dividing:
  • 4/9
  • 7/13
  Try these using the unit fractions table method, and Fraudini's trick (writing a number as a sum of distinct powers of 2).

Homework:

1. Please read this short chapter from a favorite old textbook: Mathematics: a Human Endeavor, by Harold Jacobs.
2. Do the problems on the four pages of the handout from class.
3. For extra credit, submit two pictures of yourself -- one of your "left face", and one of your "right face", as in this article. Is one good? Is one evil?

Homework:

• Please read pp. 100-103 (up to "Volumes and Calculus").
• Read "Calculating pi", if you didn't before (p. 94-95) -- one important use of regular polygons.
• To hand in (due Tuesday, 3/29):
  1. In your own words, explain why no Platonic solid has
     1. hexagonal faces
     2. octagonal faces
     You should use at least 100 words -- maybe even a diagram. This is not a "short answer" problem!

  2. Find an example of a company's logo which involves Platonic solids (don't use those you find using these resources, but they'll get you started):
     • Logos!
     • (explain how this one is related to Platonic solids)

  3. Draw 2-dimensional projections of each of the Platonic solids. That is, a realistic view of a Platonic solid on 2-dimensional paper. Try your hardest to do this well!

     Here is an example for a cube:

     

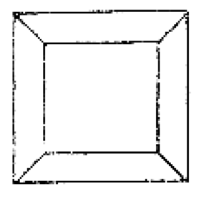
     Now you do the rest....

  4. For each of the Platonic solids, compute the following: where F is the number of faces, E the number of edges, and V the number of vertices. What do you discover?

  5. Find a soccer ball and try the same thing () on that: what do you discover?

Homework (due Tuesday, 4/5):

1. Please read a history of the recycling symbol
2. Draw by hand a mobius band, and highlight the edge in the drawing. What do you see?
3. Draw by hand a twice-twisted band, and highlight the edges in the drawing. What do you see?
4. Find a logo with a mobius band theme. Draw it on your paper, or print it off, with URL or reference.
5. Draw by hand all four links we've now encountered:
   • The unlink
   • The Hopf link
   • The Solomon's knot (actually a link)
   • The Borromean rings

Reading for next time: Knots: a handout for math circles

Homework (due Tuesday, 4/12):

• Identify the knots (or links?) in this "story", which I call A Knotty Tale. You may need to apply the Reidemeister moves to convince yourself that a picture of a knot is really the unknot, say, but you don't need to tell me how you determined which knot or link each one is. Just put a name next to each one.

  You must print off and put your answers on a copy of the knots (or else draw them meticulously by hand). Otherwise it's a zero. No exceptions.

Please read pp. 142-148 in our text for next time.

Homework (due Thursday, 4/14):

• Ordering the knots from left to right, top to bottom, use knots 3, and 12 from A Knotty Tale and the Riedemeister moves to discover what knots those are. That is, turn them into projections that we recognize.
• Draw your own version of the unknot, but one obtained from the simple circle using each of the Reidemeister moves (so that it looks confusing).

Homework (due Thursday, 4/21):

1. Please read pages pp. 187-191 (to "Axioms Again").
2. Try these problems.
3. Create your own examples of
   1. a stick fractal, and
   2. an area fractal.
   You'll need to
   • Define the simple rule (e.g. how does a stick turn into other sticks?)
   • Apply the rule at least twice, so that we can begin to see "the world within the world"

Homework (last one!): Please read pp. 78 and 79. Then, due Thursday, 4/28:

• Explain why Achilles can overtake the tortoise! Why was Zeno wrong?
• Consider the set of colors C={red, white, blue}:
  • What is the power set of C?
  • What is the cardinality of C and what is the cardinality of the power set of C?

• Explain why the power set of a finite set is always bigger than the set itself.