Day 27, MAT115

• You have an assignment on Fractals (due Thursday).
• Your first homework on knots is returned. Here's the solution, however.
  • Does Sara have any secrets to share about distinguishing knots?
  • One secret is to check for links/knots first!
  • Tricolorability is a test of trefoil.

• Your second homework on knots -- Reidemeister moves -- is not yet graded. Sorry about that: I'll have it Thursday.
• Don't forget that your logo day is coming, next Tuesday!

  From our syllabus:

  Companies have logos; you should have one, too! Your math logo will be something (like a family crest) that represents you. It will be created using elements from this course (or other mathematical elements of your own choosing). You will type up a one-page sheet, illustrating and explaining your choice. Note: correction -- the following is now false: These will be presented the last day of the course.

  Next Tuesday, not the last day. You have one week.

  The last day will be for review.

(When is "infinite love" not enough?!)

• What does infinity have to do with other topics in our course?
  

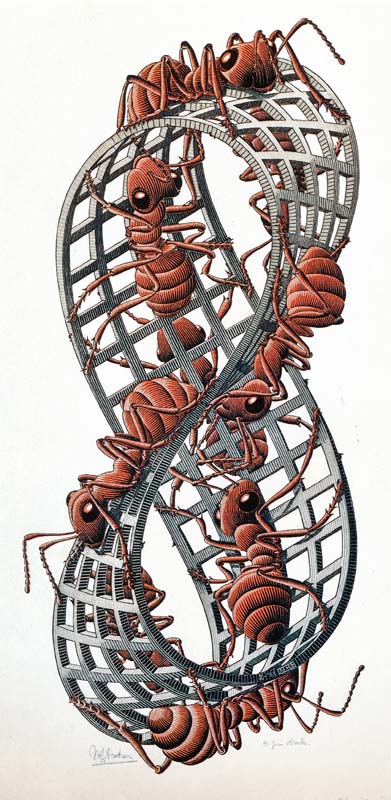
  Ants on a Mobius bands could do this forever! Fractals are infinite, in a very real sense -- maybe even infinitely beautiful. Mobius bands have mobius bands inside them (just cut them into "thirds"), and one coud do that forever.

  Eternity is tied up with the concept of infinity, frequently -- not too surprisingly.

  One Fibonacci numbers are infinite, as is the spiral (and, in the limit, when you get all the way to infinity... (wait a minute -- what does that mean?) .... then it becomes golden!).

• Something similar to the ants, but not quite:
  

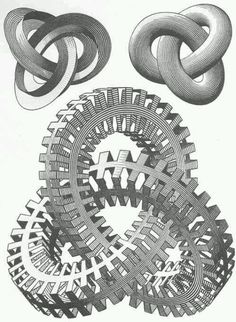
  How about lizards, mixed up with Platonic solids?

  

  

  All of these images are by the astonishing artist M. C. Escher.

• What does this line from Amazing Grace's sixth stanza have to do with this topic?
  When we've been here ten thousand years...
  bright shining as the sun,
  we've no less days to sing God's praise
  than when we've first begun.
  

  About another Newton (other than Sir Isaac): John Newton 1725-1807; ironically Newton was a slave trader (who ultimately saw the error of his ways).

• Let's look at some curious problems about the "Hilbert Hotel" (aka "Motel $\infty$")
  • The modern understanding of infinity dates to work done by Georg Cantor, in the late 1800s.

    By the way, Cantor has a fractal named after him. Cantor's "middle third" fractal.

  • David Hilbert (himself a very famous and brilliant mathematician) said "No one shall expel us from the Paradise that Cantor has Created."

    Our objective is to give you a glimpse of this paradise.

  • Welcome to the Hilbert Hotel!
    • there is a room for each natural number.
    • Everyone can be asked to move (but only once per night).

    • Notions of infinity rely on the idea of one-to-one correspondence, which you may recall from our early study of numbers.
    • Can the Hilbert Hotel really be full?
    • Hilbert Hotel and the infinite schoolbus
    • Hilbert Hotel and the limitless stable of schoolbuses

• Here's what we need to know about $\infty$:
  • infinity is NAN: not a number.

  • infinity is NAS: not a size, either! the reason is that there is more than one size of infinity! this is the most important thing I want you to remember (this fact will allow you to win on the playground, when someone tells you that they hate you an infinite amount -- you can still hate them more!;).

  • The natural numbers are infinite in number ($\aleph_0$ -- "aleph null"). As far as I know, this is the only time we mathematicians use Hebrew letters.

  • cardinality

    two sets have the same cardinality if there is a one-to-one correspondence between them.

    intuitively: two sets are the same size if they have the same cardinality.

  • Here's a sensible rule you can be sure of: a subset is never bigger in size than the set itself.

    and if the sets are finite, the proper subset is always smaller....
    but if the set is infinite, we may actually be able to throw away elements of a set and not change the size of the set!

• Are the rational numbers (ratios of integers) a bigger infinity than the natural numbers? (The natural numbers are a subset of the rational numbers.)

• The real numbers are bigger than the natural numbers, and we can prove it -- by contradiction.
  • We'll assume that they're not bigger -- that there is a one-to-one correspondence -- then show that that is impossible.
  • We'll need this fact: every real number can be expressed by an infinite decimal.
  • We need to be aware, however, that some real numbers are expressed by more than one decimal (for example, 1.00000....=0.99999.... -- did you know that?)
  • We'll show that just the real numbers between 0 and 1 are too numerous to be put in one-to-one correspondence with the natural numbers.
  • We show this using a procedure that we might call "dodge ball".

• the power set: showers of infinities!

  There are infinitely many sizes of infinity. It turns out that the power set of a set is always of larger cardinality than the set itself. Thus every infinite set is smaller than its power set, which is an infinite set, which is smaller than its power set, etc....