Day 2, Mat129: Calculus I

Speaking of which, you have an assignment due on IMath this Friday at midnight (actually 11:59 p.m.). It's optional, but will count for an extra GOHF.

Actually what will happen is this:

its grade will be counted as a homework as well, and you'll get one additional GOHF card for the course. So if you do well on the assignment, I'll end up counting that grade and dropping a lower grade; if you got a 0 on it, it would just end up being dropped. So it can't hurt you, and it might help.

• Monday-Thursday, 9-3
• Friday, 9-noon

• Mean: 14.8125
• Median: 15.5

• your form (and, near your name, the "number correct" out of 25),
• the correct answers (BBCABDAEBEDECEDACCCEAEDED) have been put in next to any that you got wrong,
• and the test is available here.

Now what do we do with the result of this diagnostic test? Compute your percentage (multiply by 4!), then reference these data (which come from the University of Kentucky: Elementary Calculus at UK: 2423 Students over Four Semesters (2002-2004)).

You might look back over the test, and see if you can identify a trend in the problems you missed. Are there things that you need to work on in order to do well in calculus?

A couple of issues:

• Time may have been a factor for some.
• Some of you are just rusty, and can knock the rust off quickly.
• Some of you might have just been nervous.
• Worst case scenario: you're not ready for calculus.

If you didn't perform well, you might want to take the Diagnostic tests in your text (p. xxiv) to see if you can get a better handle on where you're weak.

You might also make plans to spend plenty of time in the Calculus lab (MEP 457).

So hopefully you've already read section 1.5, and you're up to speed with notation.

The most important definition in calculus is the derivative (here is the derivative of $f$ at $x$):

And that's why we're so concerned about limits! Memorize it. Be able to write it at a moment's notice.

Some Review points:

• Function representation
• Variables -- independent and dependent. [In the limit above, it's actually $h$ that is the independent variable, for a fixed value of $x$.]
• Domains and Ranges
• Function composition
• Ratios!
• Indeterminate things... (division by 0)

This slide show illustrates the approach of the secant lines to the tangent line for a smooth curve. It's one of the first important problems we'll want to address in calculus. It's why we're interested in limits of things at the outset.

We usually find the equation of a line using two points, or a point and a slope. The tangent line at a point involves using a succession of nearby points that are ever closer to the point of tangency.

Question: By the way, the tangent line "osculates" the curve at this point. Do you know what "osculates" means?

Notice the focus on linear functions: linear functions are the most important functions in calculus.

Try finding the slope of the secant line when $x=2$, and check with your neighbor. Draw in the secant line.

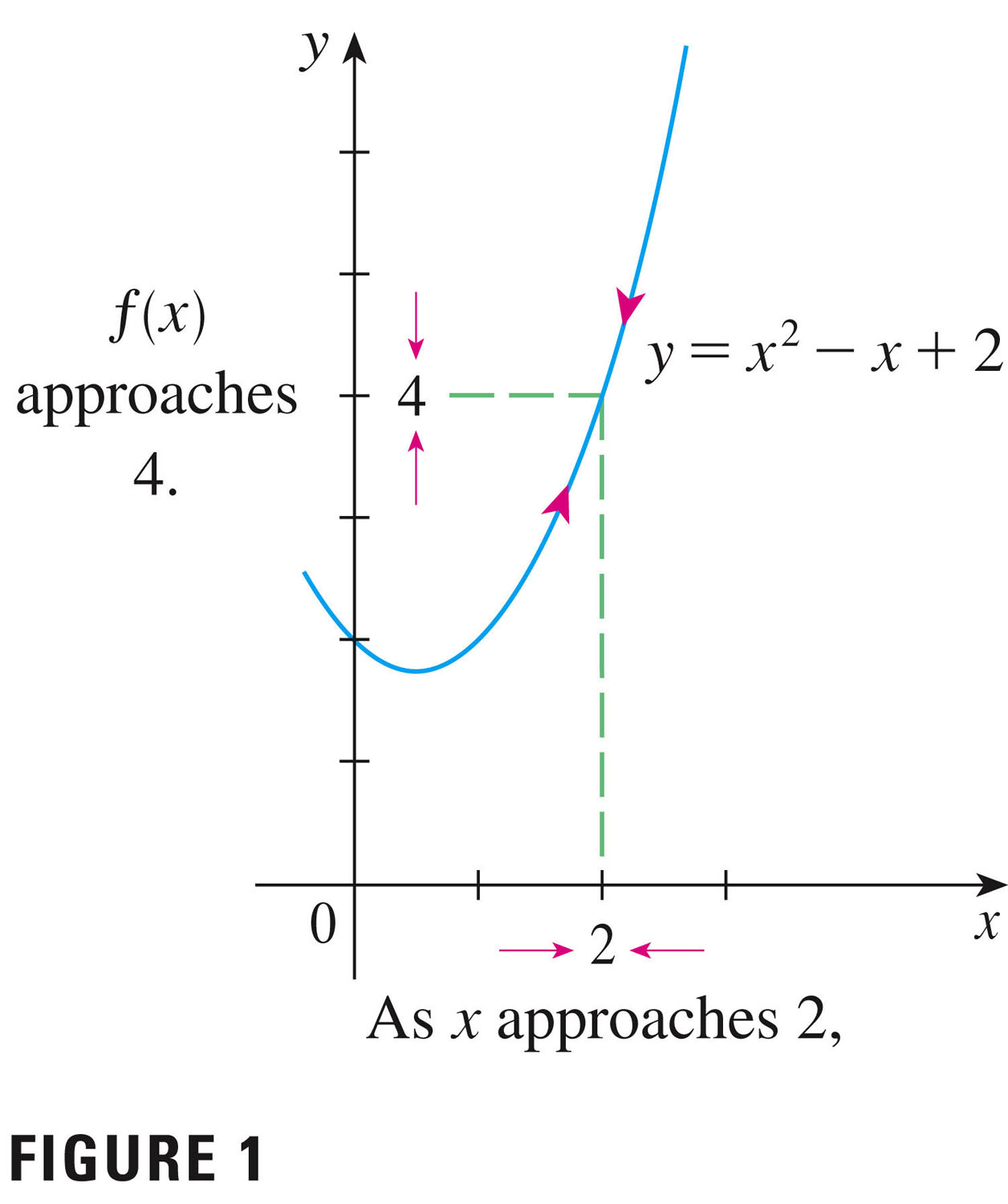
limit of $f(x)$ as $x$ approaches $a$: Suppose function $f(x)$ is defined when $x$ is near the number $a$ (this means that $f$ is defined on some open interval that contains $a$, except possibly at $a$ itself.) Then we write \[ \lim_{x \to a}f(x) = L \] if we can make the values of $f(x)$ arbitrarily close to $L$ by taking $x$ to be sufficiently close to $a$ but not equal to $a$. We say that ``the limit of $f(x)$ as $x$ approaches $a$ equals $L$.'' The intuitive idea is that in the neighborhood of $a$, the function $f$ takes on values close to $L$.

Questions:

• In the figure what is $a$, and what is $L$?
• To what class of functions does $f$ belong?
• Do limits (i.e. do we) even care about what happens exactly at $a$?

We can approach $x=a$ from the left or from the right. We define limits from the left and from the right, and then say that the limit exists as $x$ approaches $a$ if and only if the limits from the left and right exist, and agree: if \[ \lim_{x \to a^-}f(x) = L \] and \[ \lim_{x \to a^+}f(x) = L \] then \[ \lim_{x \to a}f(x) = L \]

Let's check out some Mathematica examples from section 1.5, and check out not only the limits, but also what dangers lurk, even when we have very good technology. You can't always trust your calculator; trust your brain first.

We'll be using Mathematica extensively in this class. Have I told you that you have the right to a free copy of Mathematica?

Let's take a look at a few problems from the text (pp. 59--).

• Let's check the last of the examples from section 1.5, to get started. Mathematica tells one more lie!

  So limits may be infinite (one-sided, perhaps). Here's how we define that:

  infinite limits for $\displaystyle f(x)$ as $\displaystyle x$ approaches $\displaystyle a$: \[ \lim_{x \to a}f(x) = \infty \] means that the values of $\displaystyle f(x)$ can be made arbitrarily large (as large as we please) by taking $\displaystyle x$ sufficiently close to $\displaystyle a$ (but not equal to $\displaystyle a$). Similarly we can define \[ \lim_{x \to a}f(x) = -\infty \] and one-sided limits such as \[ \lim_{x \to a^-}f(x) = \infty {\hspace{1.5in}} \lim_{x \to a^+}f(x) = \infty \]

  

  In any of these cases, we define a vertical asymptote of the curve $\displaystyle y=f(x)$ at $\displaystyle x=a$.

• #18, p. 60 -- be creative!
• #26, p. 60
• #35, p. 61
• #42, p. 61 -- one more dirty rotten lie!

  Note the symmetry, which allows us to check only one side.

  Symmetry is a very important (and under-discussed) aspect of mathematics. Keep an eye on even and odd functions.