- Your quiz is returned.
- Some of you still don't know the most important definition in calculus.
- f'(a) is the slope of a tangent line.
- The Intermediate Value Theorem
- We have an exam on Monday -- today is your chance to get your questions answered!
- You have a homework due today (2.1). But I'll be glad to go over anything on that homework.
- Four sections, 1.5, 1.6, 1.8, and 2.1
- Know definitions (especially continuity, and the most important definition in calculus)
- Know important theorems -- e.g. IVT, or squeeze theorem; the continuity of continuous compositions.
- Know the geometric definition of a derivative -- as slope of a tangent line.
- Know how to obtain an equation of the tangent line at a point.
- Know your limit laws. It's all about limits! How can limits fail to exist?
- Derivative calculations come down to figuring out how to handle an indeterminate form. Often it involves some tool from algebra.
- Section summaries:
- Let's begin by noting the difference between the derivative
at a point, and the derivative on an interval (i.e. the derivative as
function).
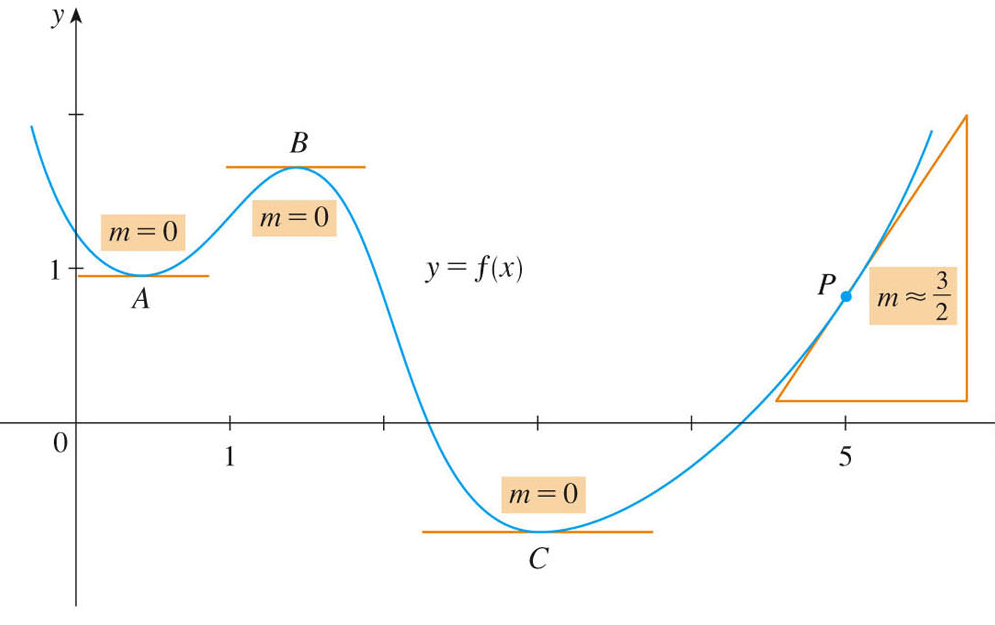
I have a handout for you to consider now, regarding this graph.
We see the derivative (thought of as a slope) at four separate points (A, B, C, and P). At three of these points we see that the slope (and hence the derivative) is zero. These are especially important points, since, as you can see, the function achieves its extreme values on a local level at these points. That's something we are often interested in -- when is a function at its peak or pit?
One of the local peaks or pits may be global as well, and if we were looking for the place along the $x$-axis where the minimum of the function occurs, we might guess $x=3$. There may be no maximum, as the values of the function on the boundary are largest (that we can see).
We can see, however, that the slope is perfectly well defined everywhere for this function (with the possible exception of the end points, where the graph disappears, and we won't have limits from left and right). Now let's see how to draw a rough approximation to the derivative function in this case.
How well can you recognize derivatives and the functions that give rise to them? Let's try #3, p. 122.
Now I'd like to use the definition of the derivative function,
\[ f^\prime(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]
to determine the derivative functions of these important functions:
- Constant functions: $f(x)=c$
- Linear functions: $f(x)=mx+b$
- Quadratic functions: $f(x)=ax^2+bx+c$
- An important application of the tangent line
If a function's derivative is another function, does that function have a derivative?
The derivative of the derivative of a function is called the second derivative of the function. And how do we interpret these "higher derivatives" in the context of a motion?
Let's think of a quadratic motion, e.g. the motion of an eraser thrown across the room. Let s be the height of the eraser:
$s(t)=at^2+bt+c$
Each of the coefficients has an important, intuitive role to play:
- $c$ is the height at time $t=0$;
- $b$ is the rate of change in height at time $t=0$;
- $2a$ is the acceleration (due to gravity) of the height.
- Here are other notations for the derivative function:
\[ f^\prime(x) = \frac{dy}{dx} = \frac{d}{dx}\left(f(x)\right)=\left(f(x)\right)'=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]
There are several different ways of writing the derivative, and you need to get used to them. The third and fourth forms remind us that differentiation is itself a function: it takes a function in its domain and returns another function in its range -- the derivative function.
- Examples:
- #2, p. 122.
- #25 (we'll finally use that thing that I call "the most important definition in calculus" in an exercise!)
- #48, p. 125.