Day 25, Mat129: Calculus I

• Your exams are returned.
  • Curve: add 3 points to your raw score (out of 60)
  • The exam
  • The key
  • Particular problems:
    1. The most important definition in calculus:
       • 5 Didn't know
       • 3 Sort of knew
       • 13 Knew
       Of those who knew, many screwed up the composition.

       Others then messed up the algebra.

       How many of you checked your answers? You know that the derivative of $x^{-2}$ is $-2x^{-3}$....

    2. Use symmetry. The first plot has to be the derivative, because it's odd, and the other two are even. Then use the zero of the derivative to decide which is which.
    3. Differentiation rules: some forgetting is going on (product rule, quotient rule). Some really bad algebra, and other things: $x\cos(x)\ne\cos(x^2)$

       or

       $x\cos(x)\ne\cos^2(x)$

       You can't slip that $x$ into the argument of $\cos(x)$. By the way, all trig functions need arguments: $\sin$ is a sin, not a sine. $\sin$ is a hungry operator, and needs something to eat: e.g. $\sin(x)$. We say "Sine of $x$" -- the "of" is the hunger: sine of what?

       One more issue (two people, at least):

       $\frac{\sin(x)-x\cos(x)}{\sin(x)^2}\ne\frac{-x\cos(x)}{\sin(x)}$

       We might call this "over-simplification"....

    4. Ditto for tangent: $\tan$ is a tan, not a tangent; it needs an argument, too: $\tan(\frac{1}{x})$.
    5. Some of you did both. Read the question! Choose one! Watch units.
    6. At least five people factored $3(x^2+2x-3)$ to get $3(x-2)(x-1)$...?!

       We have a serious algebra problem here....

       Use the quadratic formula. It always works.

       Your sketch should be of a cubic. If you know what cubics look like, you're way ahead; if you don't, you're behind.

       The Extreme Value Theorem guarantees that there will be global max and min on this interval.

• There's a homework due today (and one due next time).

• Let's meet here on Friday, rather than in the lab. We're still playing catch-up.

So now we know how to handle closed, bounded intervals; now let's talk about what happens when we let $x$ become unbounded. How will a function behave as $x$ races off to $\infty$ or $-\infty$?

• Examples of functions without finite limits at infinity:
  • non-constant polynomials (go to infinity, in the positive or negative sense)
  • the usual trig functions (while sine and cosine are bounded, but don't settle down to some nice limiting value)

• But rational functions may have horizontal asymptotes, as do exponential functions.

  Another example with a horizontal asymptote is knowledge as a function of time -- #51, p. 222. We might guess that accumulated knowledge in studying for an exam looks something like this:

  

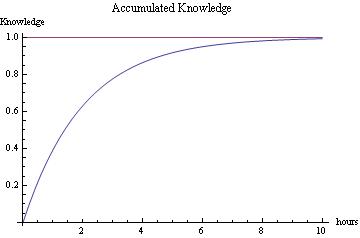
  We might imagine that this physical process becomes less productive from hour to hour as the evening wears on (the law of diminishing returns).

  Other Examples:

  • The hyperbola: $f(x)=\frac{1}{x}$

    More generally, If $r>0$ is a rational number, then

    $\lim_{x \to \infty} \frac{1}{x^r}=0$ If, furthermore, $x^r$ is defined for negative numbers, then $\lim_{x \to -\infty} \frac{1}{x^r}=0$

  • The most general form of an hyperbola is this: $f(x)=\frac{ax+b}{cx+d}$
    • What is its horizontal asymptote?
    • Where is its vertical asymptote?

  • A rational function will have a horizontal asymptote any time that the degree of the denominator equals or exceeds that of the numerator: if
    $r(x)=\frac{p(x)}{q(x)}$

    then if the degree of q exceeds that of p, there is a horizontal asymptote, and the value of the asymptote is given by examining the approximating function given by the ratio of leading terms alone.

  • Interestingly enough, if the degree of the numerator ($n$) exceeds that of the denominator ($m$), then the rational function ultimately looks like a polynomial of degree $n-m$: for example, consider the function $f(x)=\frac{x^2-1}{x}$. Its graph will ultimately look a lot like the function $g(x)=x$ (which one can determine by (gasp!) long division....

    This is called a "slant asymptote" (not a horizontal asymptote, for obvious reasons! If you get far from the origin, then the difference between the two functions falls away.

    We can then replace the more complicated with the simpler.

    We use this idea in physics all the time: we assume that gravity is constant at the surface of the Earth. In fact, it varies as distance to the center of the Earth, but we're so far away that we can take this as a constant (its value at about 4000 miles -- our distance to the center of the Earth). We're far enough from the origin (the center of the Earth) that we treat acceleration due to gravity as locally constant.

  • The usual rules of limits apply, with the caveat that one must be careful when dealing with $\infty$. It is not a number, and cannot be added to anything else (e.g. it is not valid to write that $\infty-\infty=0$ -- for example, $x^2$ and $x$ both go to infinity, but their difference, $x^2-x$, also goes to infinity).

    We can say, however, that $\infty*\infty=\infty$, that $\infty*1=\infty$, that $\infty/1=\infty$, etc. So some of the usual rules apply (and hopefully make sense!).

• Examples:
  • #7, p. 234
  • #11
  • #16
  • #44 (re-express the function first, and use symmetry!)
  • #49 (factor first, and use symmetry!)

• You will notice that this section includes the "new" technique of the calculation of "slant asymptotes" (which we just discussed).

  This is just one type of asymptotic behavior that is sometimes useful. In fact, as mentioned in the previous section, every rational function approaches a polynomial in its end behavior, so that we're interested here in those rational functions (and some others) which approach linear functions as x gets large.

  E.g.,

  $f(x)=\frac{x^2-4x+17}{x-3}$

  Or even non-rational functions, such as

  $f(x)=3x-6 + \frac{\sin(x)}{x}$

• So here's the upshot on the graphing of functions, "the strategy":
  1. Look at the expression of the function: can you simplify it in any way?
  2. Domain -- find it.
  3. Symmetry -- hope for it!
     • even and odd functions;
     • functions that have symmetry about some displaced point;
     • periodicity.

     These help to reduce the amount of work we have to do.

  4. Intercepts - crossings of the axes. The y-intercept is the point $(0,f(0))$ (if 0 is in the domain); the x-crossings are the roots of the equation $f(x)=0$: The special values of x that make this so.
  5. Asymptotes - vertical, horizontal, slant
  6. Intervals of increase or decrease - consult the sign of the first derivative.
  7. Local maxima and minima - use the first or second derivative tests.
  8. Concavity and points of inflection - use the second derivative and the concavity test.
  9. Compute some points on the curve, especially any that are trivial to calculate, or especially interesting.
  10. Sketch the curve - sketch asymptotes as dashed lines; plot any known points on the curve (e.g. intercepts); finish by connecting the points in accord with the information above.

      Use anything that you know about the form of the function to help inform your graph (e.g. if you know it's cubic, then you already have a good idea what it's going to look like).

      If your function is periodic, then you only need to sketch it on one period.

• Examples:
  • #9, p. 242
  • #12, p. 242
  • #23 (use completion of the square to get the asymptotic behaviour)
  • #50, p. 243