Day 39, Mat129: Calculus I

Last time:

Next time:

Today:

Announcements
- Your 4.3 homework is returned: graded 12, 14, 21.
- Your 4.4 homework is due today, , and 4.5 for next time.
- Your exam revisions are also due on Wednesday. Sorry to keep you so busy, but we're in the home stretch!
We've finished up Section 4.5: The substitution rule (for solving selected integrals analytically)
Now we're looking at several applications of integration: why are integrals so important?
Last time I shared how we can solve one of my favorite problems using integral: hose signs you see on the highway, that tell you the time to this or that road, or this or that exit. How can they do that?

How do they know how long it's going to take you today?
An engineer with an integral (and some sensors) can tell you! Let's think about how.
All integrals start out this way: $T = \int dT$
If we were doing
- mass, then I would write $M = \int dM$
- force, then I would write $F = \int dF$
- energy, then I would write $E = \int dE$
etc. We think of the quantity of interest made up of chunks of stuff, then figure out how to add it up.
When we're introduced to integration, we usually think of our integrals as area, so we might write $A = \int dA$
and then we think of $dA$ as small rectangles: $dA=f(x)dx$ as a rectangle of height $f(x)$ and width $dx$, as $x$ varies from $a$ to $b$:
$A=\int_a^bf(x)ds$
It's the limit of this picture,

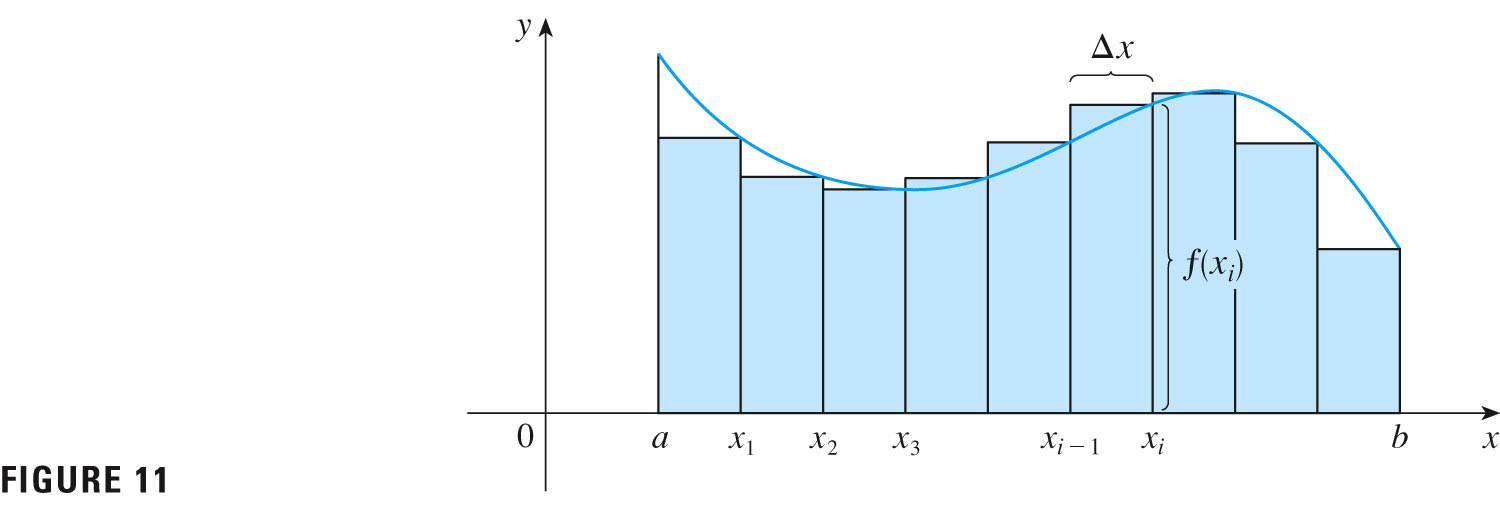
as the widths of the rectangles $\Delta x$ go to zero.
Today's new topic: Section 5.1: the area between curves
There's no great shakes here: we continue to think of integrals as representing areas. In our introduction to the integral, we've begun by thinking of a definite integral as representing a signed area, between a curve and the x-axis. Now suppose that we want the area between two curves:

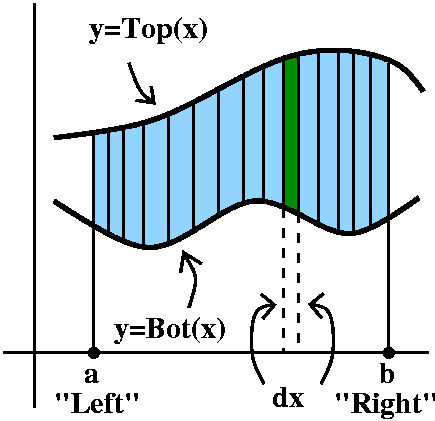
If one curve is always above the other, then we simply subtract the smaller area from the larger:

If the top curve is the graph of $f(x)$, and the bottom curve is the graph of $g(x)$, then the difference in the areas, which is what we want (in blue), is

$I=\int_{a}^{b}f(x)dx-\int_{a}^{b}g(x)dx = \int_{a}^{b}(f(x)-g(x))dx$
Let's do some examples.
There are a couple of tricks here:
1. One is to figure out what to do when two curves cross:
  
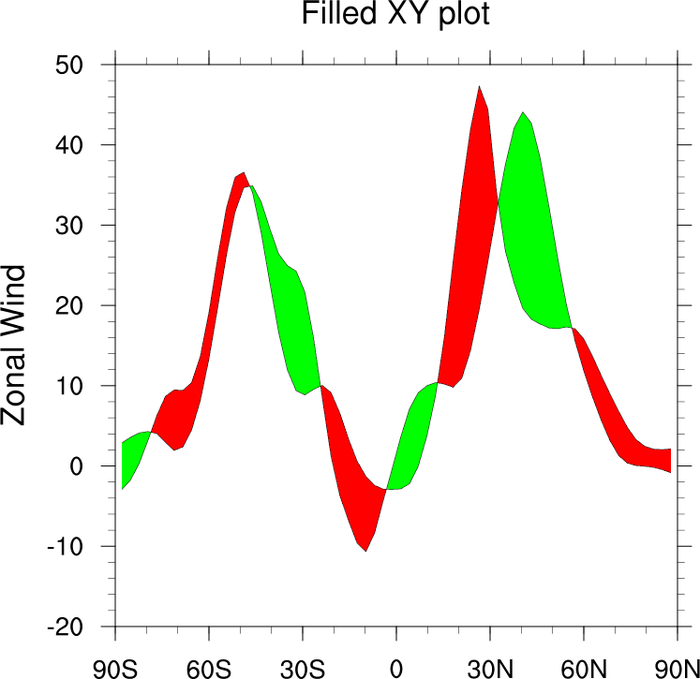
  In this case, the sign of the area changes as ${f}$ and ${g}$ change roles (which one is above, which below). If we want the actual geometric area, and not the signed area, then we can use this formula:
  
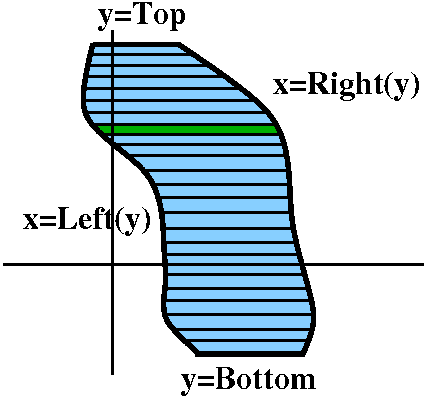
  $I = \int_{a}^{b}\left|f(x)-g(x)\right|dx$
2. The other trick is integrating along the y-axis, rather than along the x-axis.
We'll try examples of both.
- #2, p. 349
- #3
- #6
- #17 (switch roles!)
- #31
- #41
- #45
- #46

Website maintained by Andy Long. Comments appreciated.