Day 43, Mat129: Calculus I

• Your 5.1 homework is graded: pp. 349, #5, 14, 28
• Thanks to Felix for alerting me that a new class -- mat128! -- has been added to your Blackboard courses. That is an assessment, which
  • will be available today, evidently;
  • will count as two homework assignment GOHF cards, if you do it (and all I'll know is whether you did it or not);
  • will not affect your grade otherwise. Do your best, that's all I'd ask: take it seriously.

• Your 5.2 homework may be turned in at the time of your final, and will count as a homework replacement for a lower one.

• Today: review of new material
• Friday: review of all material
• Sunday night, 7:00-9:00p.m.: review, here.
• Monday: I'll be in from about 8:00 through exam time.

1. A second type of volume integral
2. A mass problem
3. A work problem

But in each case, we have a different type of quantity that we're after:

1. A volume integral: $V=\int{dV}$
2. A mass problem: $M=\int{dM}$
3. A work problem: $W=\int{dW}$

• The sphere is of radius 2 meters.
• The center of the sphere is 20 meters above the surface of the source of water.
• Water has a density of $1000kg/m^3$

• Work is technically defined as force times displacement: W=F*d
• In this case, we have the force of gravity lifting layers of water up to the tower: dW=F*dh

As an example of using integrals to do practical or interesting things (such as find the time to travel to exit 16), let me give you an example from my own life. Sometimes it just provides a context for a way to think about a problem....

I was thinking this morning about my desire to help heal the damage that humans have done to the Earth. But I do damage myself, even as I try to undo damage.

So I started this way:

But this is really a function of time, so that, at any moment,

Sometimes we'll do short term damage, in order to make a long-term gain. So it's really this function over my lifetime that is of interest (and perhaps only my "conscious" lifetime, starting from some $t_0$ and ending at $t_f$:

• Section 4.3: the Fundamental Theorem of Calculus
• Section 4.4: Indefinite integrals
• Section 4.5: Substitution
• Section 5.1: Areas between curves
• Section 5.2/5.3: volumes (by cross-section and cylindrical shells)
• "Other applications"

1. Find $\int_0^1 \frac{x}{\sqrt{4-x^2}} dx$, without recourse to the calculator. In other words, show all steps.
2. Now, using your calculator, approximate $\int_0^1 \frac{x}{\sqrt{4-x^2}} dx$ using $R_{2}$, $L_{2}$, $M_{2}$, $T_{2}$ and $S_{2}$.
3. Consider the positive region bounded by the y-axis, the function $x^2$, and the function $2-x$, as seen in the following figure. Compute the volume of the object obtained by rotating this region about the y-axis, in two different ways: using cylindrical shells and using disks/rings.
   

4. A population of a large city is radially symmetric about the city center. Its population density can be modelled well with the density function $\rho(r)=\frac{1}{r^2+1}$, in units of millions of people per square mile, and where $r$ is the distance from the center. Compute the total population within the area 10 miles from the city center.

5. For the function $f(x) = \sqrt{x}+3x^2-\cos(x)$
   1. Find all anti-derivatives of $f$.
   2. Find the particular anti-derivative whose value at $x=0$ is 2.

6. For the following integrals, indicate the substitutions you would use to compute the integrals, and rewrite the integral using the substitution (if necessary - that is, if the integral is not obvious or undefined). No need to evaluate the integrals.
   1. $\displaystyle \int_{-3}^{3} x \sin(x^2)dx$

   2. $\displaystyle \int \cos(x) \sin^3(x)dx$

   3. $\displaystyle \int_{-4}^{-1} \frac{x}{\sin(x^2)}dx$

   4. $\displaystyle \int_{}^{} \frac{x-1}{\sqrt{(x^2-2x-5)}}dx$

7. Compute the derivatives (with respect to $\displaystyle x$) of the following functions:
   1. $\displaystyle \int_{x}^{1}t^2\sin(t)dt$

   2. $\displaystyle \int_{1}^{x^2}\frac{t}{5t-3}dt$
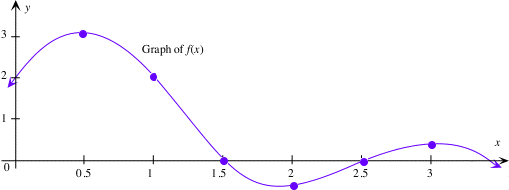
8. Let $\displaystyle f(t)$ be given by the following graph. Draw a reasonable graph of $\displaystyle g(x)=\int_{0}^{x}f(t)dt$ on the same axis:
   

9. Draw the region bounded by the two curves $y=20-x^2$ and $y=x^2-12$, then find the area of the bounded region.