- No quiz today; but generally we'll have quizzes at the end of the hour on Thursdays (when we're not having exams).
- Section 001: I need your diagnostic KEMTP tests and solutions, please (also new folks in Section 002).
- Today we'll
- finish our review from last time
- begin working on section 1.5
- You have a new assignment -- some problems from the textbook, which will be due next Thursday. You also have some assignments on IMath.
- No class Monday -- have a happy MLK, Jr. Day!
- Last time I described how calculus, which comes in two parts, can
be compared to a speedometer and an odometer. Differential
calculus concerns itself with derivatives, which are rates --
like speeds -- so that is the speedometer part; integral
calculus concerns itself with accumulated distance, which is
the odometer part.
- We started last time with a review of important notions about
functions. What is a function?
- Then we talked about important classes of functions, the most
important of which is a linear function.
- Here is a summary so far, plus some other unusual functions which
we should note:

Let's observe a few things:
- symmetry: even and odd functions are represented here
- Even: symmetric about the y-axis:
- Odd: symmetric about the origin by rotation of 180 degrees:
- Even: symmetric about the y-axis:
- Functions with restricted domains.
- Functions with corners (in particular, the absolute value).
- Functions with breaks (discontinuities), either infinite or finite. For those of you with a computer science background, the Greatest integer function is sometimes called the "floor" function.
- symmetry: even and odd functions are represented here
- Trigonometric functions
- capture oscillatory behavior
- Are periodic (repeat in space or time).
- You should know important properties of sine and cosine
(p. 31), and be able to draw them at the drop of a hat! By the
way, sine is an odd function; cosine is even. And tangent blows
up (or down) whenever cosine is 0, since
\[
\tan(x)=\frac{\sin(x)}{\cos(x)}
\]
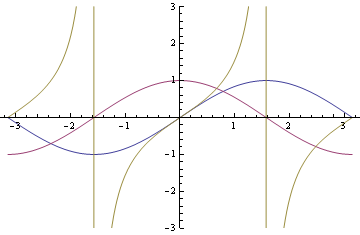
You can see that sine and cosine are just shifts of one another. We could really get by with just one or the other, but we like to have both handy.
- We see the need for a trigonometric function in the example below.
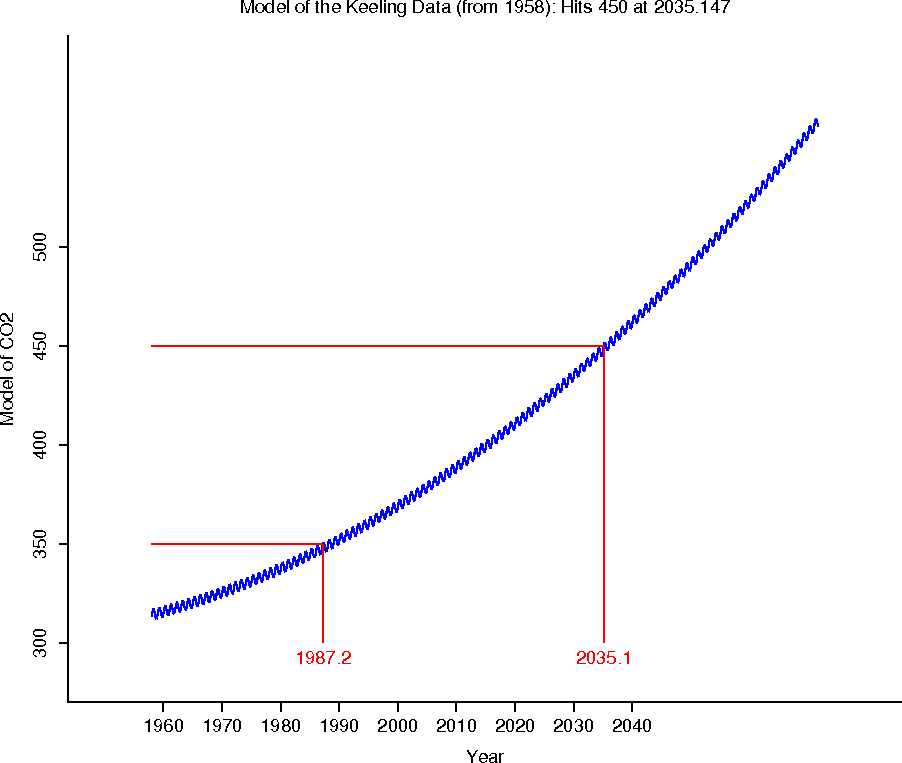
- In the end we may mix up the members of the function zoo in a model. For
example, which members might play a role in doing a really good job of
modelling the Keeling data from Mauna Loa?

Here are several of my current models of the trend, using a quadratic:
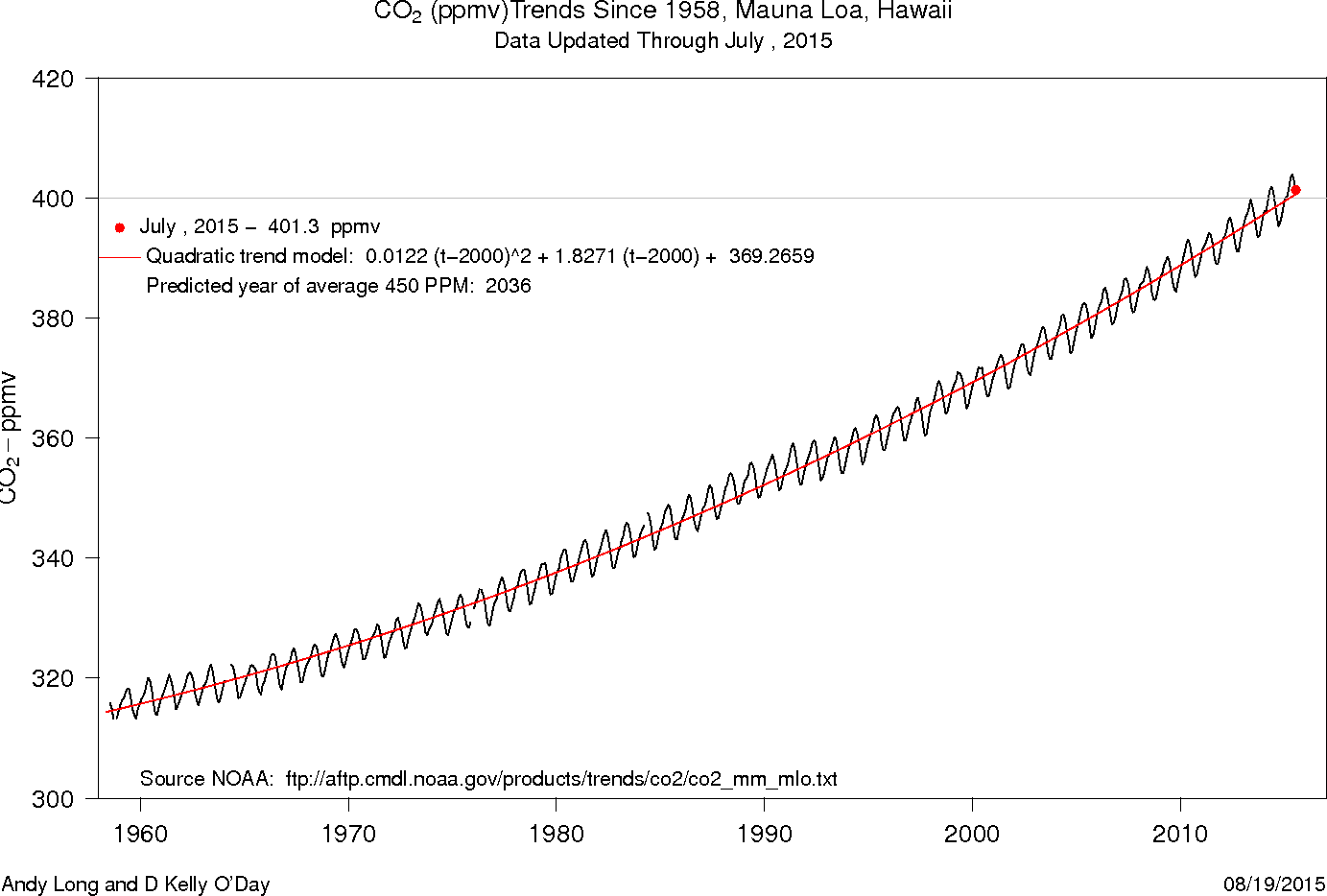

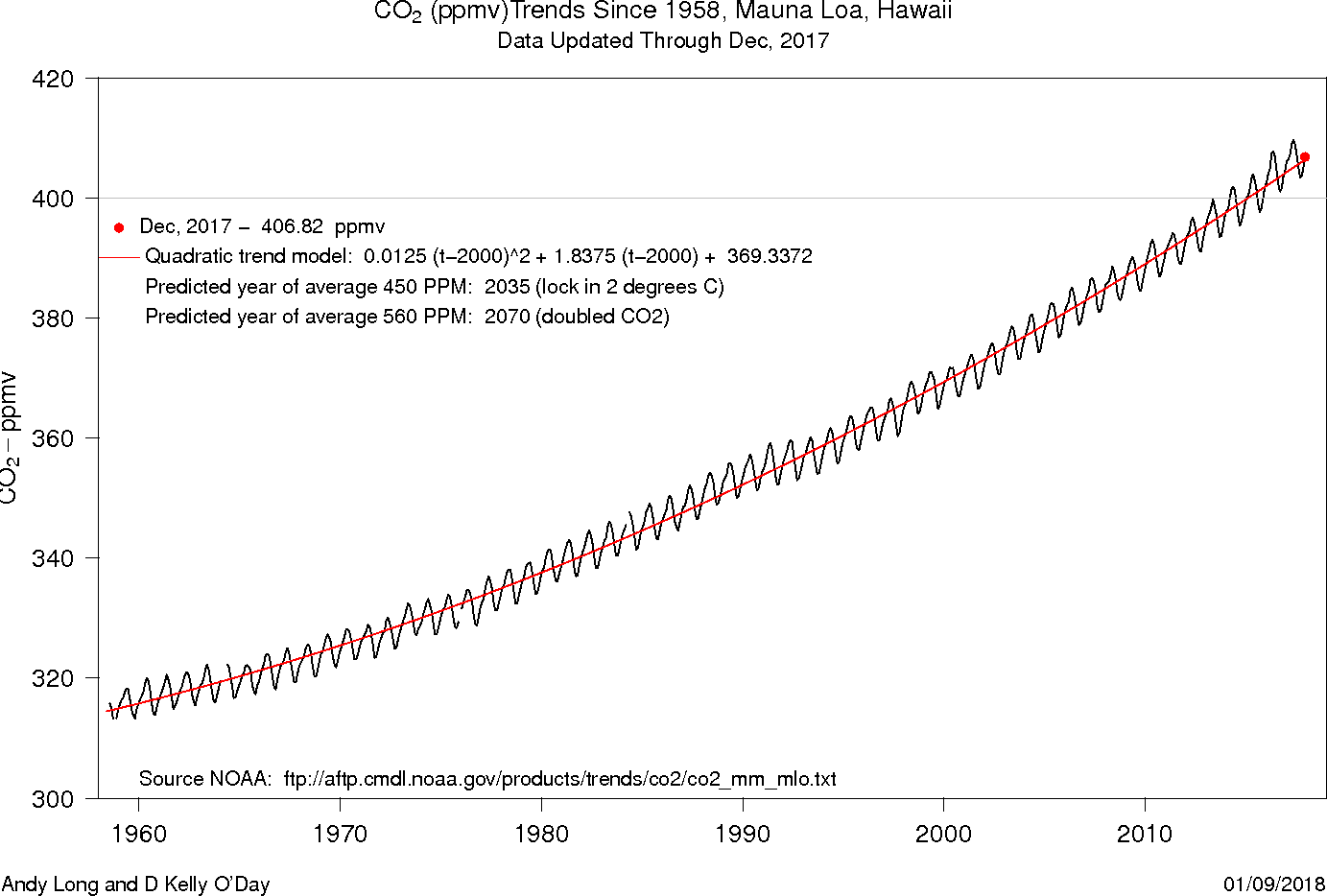
and here is one using a quadratic for the trend, but including the oscillations modelled by a sine function:
- Now, on to section 1.4: instantaneous velocity (and tangent lines)
The instantaneous velocity is a curious idea: how fast are we going at exactly this moment? Here's a graph of one of Usain Bolt's 100 meter races from 2008:
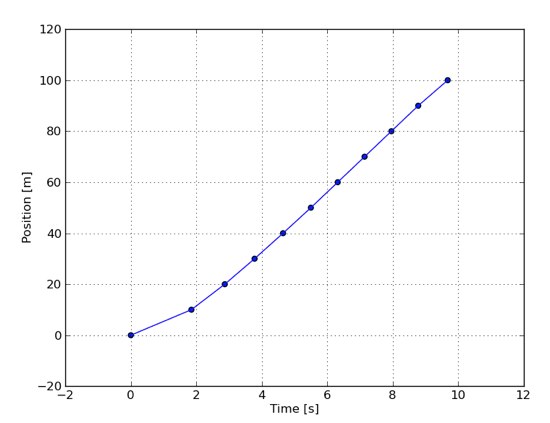
A race usually concludes with a time, but we can turn it into an average velocity, instead: Bolt ran at an average rate of about
$\frac{100m}{9.8s}=10.02\frac{m}{s}$ Do you really think that there are corners in his progress (e.g. at 2 seconds)? We don't believe that -- we just don't have data at every moment -- the more data we have, the smoother this graph will look.
In calculus we talk about limits: we'd like to have an unlimited supply of data -- data at every instant -- but that would be an infinite amount of data to plot, which would take infinitely long -- and we're just not that patient.
So we try to predict what the graph would look like "in the limit", where the difference between data values goes to zero. The limiting difference becomes "infinitesimally small"; becomes zero, essentially.
- Why are we concerned with "limits"? Sir Isaac Newton, one of the
creators of calculus, claimed that the limit is the basic concept in
calculus (see historical side note, p. 64): quantities "approach nearer
than by any given quantity".
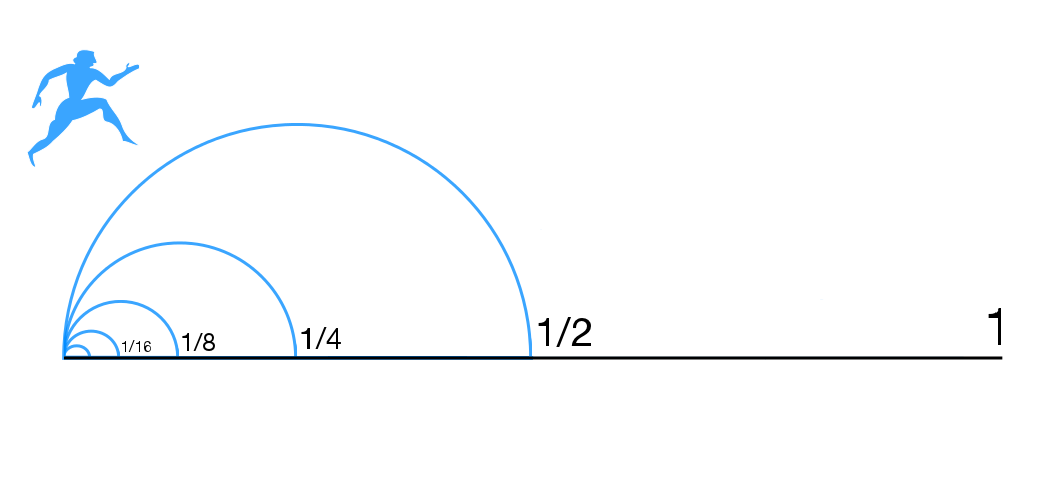
- Zeno of Elea created some paradoxes thousands of years ago that involved
limits in important ways, but mathematicians apparently didn't take the
hint very quickly. I'd like to share one paradox, that shows that motion is
impossible...:)
- This slide
show illustrates the approach of the secant lines to the tangent
line for a smooth curve. It's one of the first important problems
we'll want to address in calculus. It's why we're interested in
limits of things at the outset.
Notice the focus on linear functions: linear functions are the most important functions in calculus.
- Let's look at some examples from 1.4, using Mathematica. We'll be
using Mathematica extensively in this class, so the sooner you get your
copy, the better!
- Today we finally begin section 1.5: The Limit of a Function.
- By the way, you see the link above -- it's a link to a summary of
the section. You might want to take a look at that sometime, to see
what I think is the most important part of a section of your text.
There are a few definitions and even a theorem that we should check out there, today.
It doesn't mean that you shouldn't read the text, however!
- So hopefully you've already read section 1.5, and you're up to speed
with notation. Let's talk notation in our most important case (a
preview -- this definition is actually not in 1.5, but it's so
important that I can't wait!):
The most important definition in calculus is the derivative function (here is the derivative of $f$ at $x$):$f'(x)=\lim_{h\to 0}{\frac{f(x+h)-f(x)}{h}}$ And that's why we're so concerned about limits! Memorize it. Be able to write it at a moment's notice.
It turns out that the slope of the tangent line to a curve (provided the tangent line exists) at a particular point $x=a$ is
$f'(a)=\lim_{x\to a}{\frac{f(x)-f(a)}{x-a}}$ You can see the slope in there, for the secant line connecting the two points $(x,f(x))$ and $(a,f(a))$.
But if we define $h=x-a$ to be the distance (positive or negative -- left or right) between $x$ and $a$, then $x=a+h$ and we can rewrite
$f'(a)=\lim_{h\to 0}{\frac{f(a+h)-f(a)}{h}}$ Now it looks more like the derivative function definition.
Some Review points:
- Function representation
- Variables -- independent and dependent. [In the first limit above, the independent variable is actually $h$ for a fixed value of $x$.]
- Domains and Ranges
- Function composition
- Ratios!
- Indeterminate things... (division by 0)
- Now what is our first practical illustration of limits? The
calculation of slopes of tangent lines.
The derivative of a function at a point gives the slope of the tangent line there -- provided it exists!
We've seen how the secant lines approach the tangent line for a smooth curve. It's one of the first important problems we'll want to address in calculus. It's why we're interested in limits of things at the outset.
We usually find the equation of a line using two points, or a point and a slope. The secant line method approaches the tangent lin at a point by using a succession of nearby points that are ever closer to the point of tangency.
The tangent ("touching") line osculates ("kisses") the curve at this point.
Notice the focus on linear functions: linear functions are the most important functions in calculus.
- We begin our work in section 1.5 with p. 50, and Figure 1: this
figure presents us with the basic idea.
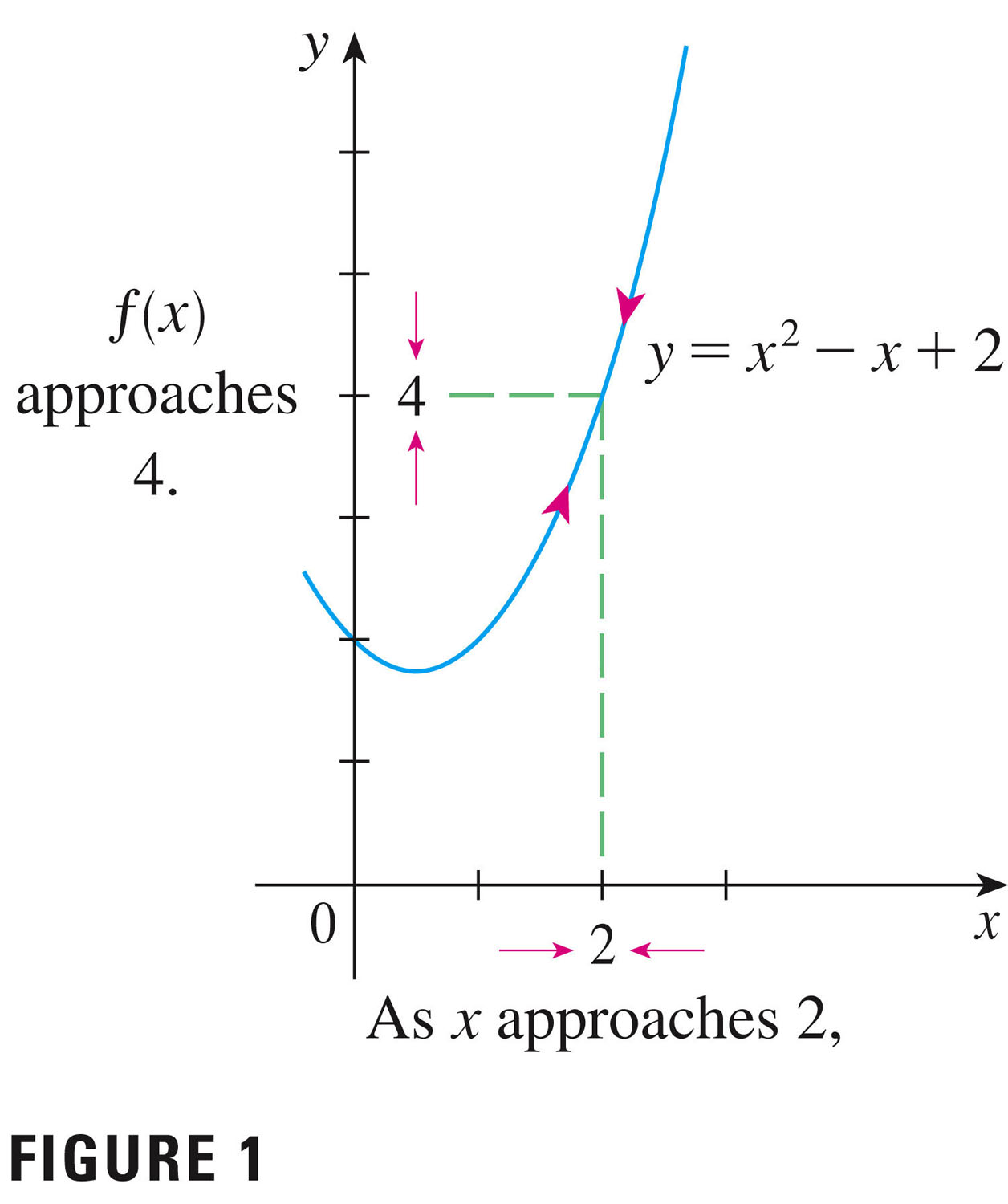
Definition (of the most important concept in calculus!): limit of $f(x)$ as $x$ approaches $a$: Suppose function $f(x)$ is defined when $x$ is near the number $a$ (this means that $f$ is defined on some open interval that contains $a$, except possibly at $a$ itself.) Then we write \[ \lim_{x \to a}f(x) = L \] if we can make the values of $f(x)$ arbitrarily close to $L$ by taking $x$ to be sufficiently close to $a$ but not equal to $a$. We say that ``the limit of $f(x)$ as $x$ approaches $a$ equals $L$.'' The intuitive idea is that in the neighborhood of $a$, the function $f$ takes on values close to $L$.
Questions:
- In the figure what is $a$, and what is $L$?
- To what class of functions does $f$ belong?
- Do limits (i.e. do we) even care about what happens exactly at $a$?
We can approach $x=a$ from the left or from the right. We define limits from the left and from the right, and then say that the limit exists as $x$ approaches $a$ if and only if the limits from the left and right exist, and agree: if \[ \lim_{x \to a^-}f(x) = L \] and \[ \lim_{x \to a^+}f(x) = L \] then \[ \lim_{x \to a}f(x) = L \]
Let's take a look at a few problems from the text (pp. 59--).
Let's check out some Mathematica examples from section 1.5, and check out not only the limits, but also what dangers lurk, even when we have very good technology (see Example 2, Figure 5, p. 52). You can't always trust your calculator; trust your brain first.
We'll be using Mathematica extensively in this class. Have I told you that you have the right to a free copy of Mathematica?
- Infinite limits
- Let's check the last of the examples from
section 1.5, to get started. Mathematica tells one more lie!
So limits may be infinite (one-sided, perhaps). Here's how we define that:
infinite limits for $\displaystyle f(x)$ as $\displaystyle x$ approaches $\displaystyle a$: \[ \lim_{x \to a}f(x) = \infty \] means that the values of $\displaystyle f(x)$ can be made arbitrarily large (as large as we please) by taking $\displaystyle x$ sufficiently close to $\displaystyle a$ (but not equal to $\displaystyle a$). Similarly we can define \[ \lim_{x \to a}f(x) = -\infty \] and one-sided limits such as \[ \lim_{x \to a^-}f(x) = \infty {\hspace{1.5in}} \lim_{x \to a^+}f(x) = \infty \]

In any of these cases, we define a vertical asymptote of the curve $\displaystyle y=f(x)$ at $\displaystyle x=a$.
- Let's check the last of the examples from
section 1.5, to get started. Mathematica tells one more lie!
- Further Examples:
- #18, p. 60 -- be creative!
- #26, p. 60
- #35, p. 61
- #42, p. 61 -- one more dirty rotten lie!
Note the symmetry, which allows us to check only one side.
Symmetry is a very important (and under-discussed) aspect of mathematics. Keep an eye on even and odd functions.
- By the way, you see the link above -- it's a link to a summary of
the section. You might want to take a look at that sometime, to see
what I think is the most important part of a section of your text.