- Your linearization labs from before Spring break
are returned.
- Taylor series are good local approximators: they don't do well (typically) when one moves "too far" from $x=a$, the point at which they are constructed.
- Part 3 was the key....
- Midterm grades:
- A biased towards your one exam -- and remember that a better final grade can replace your worst hourly exam.
- I threw away your lowest three quizzes, homeworks, and imath homeworks to estimate the rest of your grade.
- Please put your rectangles away.
- So now we know how to handle closed, bounded intervals; now let's
talk about what happens when we let $x$ become unbounded. How will a
function behave as $x$ races off to $\infty$ or $-\infty$?
- Examples of functions without finite limits at infinity:
- non-constant polynomials (go to infinity, in the positive or negative sense)
- the usual trig functions (while sine and cosine are bounded, but don't settle down to some nice limiting value)
- But rational functions may have horizontal asymptotes, as do
exponential functions.
Another example with a horizontal asymptote is knowledge as a function of time -- #51, p. 222. We might guess that accumulated knowledge in studying for an exam looks something like this:
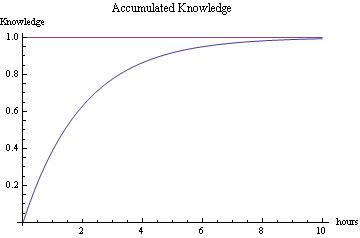
We might imagine that this physical process becomes less productive from hour to hour as the evening wears on (the law of diminishing returns).
Other Examples:
- The hyperbola: $f(x)=\frac{1}{x}$
More generally, If $r>0$ is a rational number, then
$\lim_{x \to \infty} \frac{1}{x^r}=0$ If, furthermore, $x^r$ is defined for negative numbers, then$\lim_{x \to -\infty} \frac{1}{x^r}=0$ - The most general form of an hyperbola is this: $f(x)=\frac{ax+b}{cx+d}$
- What is its horizontal asymptote?
- Where is its vertical asymptote?
- A rational function will have a horizontal asymptote
any time that the degree of the denominator equals or
exceeds that of the numerator: if
$r(x)=\frac{p(x)}{q(x)}$ then if the degree of q exceeds that of p, there is a horizontal asymptote, and the value of the asymptote is given by examining the approximating function given by the ratio of leading terms alone.
- Interestingly enough, if the degree of the numerator ($n$)
exceeds that of the denominator ($m$), then the rational function
ultimately looks like a polynomial of degree $n-m$: for
example, consider the function
$f(x)=\frac{x^2-1}{x}$. Its graph will ultimately look a lot
like the function $g(x)=x$ (which one can determine by
(gasp!) long division....
This is called a "slant asymptote" (not a horizontal asymptote, for obvious reasons! If you get far from the origin, then the difference between the two functions falls away.
We can then replace the more complicated with the simpler.
We use this idea in physics all the time: we assume that gravity is constant at the surface of the Earth. In fact, it varies as distance to the center of the Earth, but we're so far away that we can take this as a constant (its value at about 4000 miles -- our distance to the center of the Earth). We're far enough from the origin (the center of the Earth) that we treat acceleration due to gravity as locally constant.
- The usual rules of limits apply, with the caveat that one
must be careful when dealing with $\infty$. It
is not a number, and cannot be added to anything else (e.g. it
is not valid to write that $\infty-\infty=0$ -- for example,
$x^2$ and $x$ both go to infinity, but their difference,
$x^2-x$, also goes to infinity).
We can say, however, that $\infty*\infty=\infty$, that $\infty*1=\infty$, that $\infty/1=\infty$, etc. So some of the usual rules apply (and hopefully make sense!).
- The hyperbola: $f(x)=\frac{1}{x}$
- Examples of functions without finite limits at infinity:
- Examples:
- #7, p. 234
- #11 (quick!)
- #16
- #44 (re-express the function first, and use symmetry!)
- #49 (factor first, and use symmetry!)
- This section includes one new technique: the calculation of what
are called "slant asymptotes" (which I've already mentioned in
connection with the preceding section).
This is just one type of asymptotic behavior that is sometimes useful. In fact, every rational function approaches a polynomial in its end behavior, so that we're interested here in those rational functions (and some others) which approach first degree (linear) polynomials as x gets large.
E.g.,
\[ f(x)=\frac{x^2-4x+17}{x-3} \]
Even non-rational functions, such as
\[ f(x)=3x-6 + \frac{sin(x)}{x} \]
can approach linear functions.
- So here's the upshot on the graphing of functions, "the strategy":
- Domain -- find it.
- Symmetry -- hope for it!
- even and odd functions;
- functions that have symmetry about some displaced point;
- periodicity.
These help us reduce the amount of work we have to do
- Intercepts - crossings of the axes. The y-intercept is the point (0,f(0)) (if 0 is in the domain); the x-crossings are the roots of the equation f(x)=0: The special values of x that make this so.
- Asymptotes - vertical, horizontal, slant
- Intervals of increase or decrease - use the Increasing/Decreasing Test, based on the sign of the first derivative.
- Local maxima and minima - use the first or second derivative tests.
- Concavity and points of inflection - use the second derivative and the concavity test.
- Compute some points on the curve, especially any that are easy to calculate.
- Sketch the curve - sketch asymptotes as dashed lines; plot any known points on the curve (e.g. intercepts); finish by connecting the points in accord with the information above.
- Examples:
- #50, p. 243
- #58, p. 243
- #23 (use completion of the square to get the TWO slant asymptotes)