- Your exam revisions are due Monday.
- You also have a homework due then (and a slew to follow, right up to the end of class...:(
- There's a major/minor lunch tomorrow! Come out and feast at our
expense, even if you're not one of our major/minors. Tell 'em Long sent
you.
- There's a quiz at the end of the hour (anti-derivatives).
- If we know the rate at which something proceeds, e.g. the rate at
which we're pumping carbon into the atmosphere, then we may want to
know how much we've actually pumped into the atmosphere over a given
period. This is the job of anti-differentiation: given the rate of
change of $p(t)$, $\frac{dp}{dt}$ from $t=0$ to $t=T$, find the amount
pumped in over the same period: $p(T)-p(0)$.
- Whereas differentiation is essentially a mechanical exercise,
anti-differentiation may require insight, and broad exposure to
lots of different functions. One asks oneself this essential
question:
"Do I know a function whose derivative looks like this?" Note: I tend to hyphenate "anti-differentiation", whereas our author doesn't. I sometimes do, and sometimes don't. But I actually think that it deserves the hyphen....
- Definition:
A function $F$ is called an anti-derivative of $f$ on an open interval $I$ if $F^\prime(x) = f(x)$ for all $x$ in $I$. - All anti-derivatives are the same up to a constant:

- Differential Equations:
- A differential equation is an equation linking a function and its derivative(s).
The simplest differential equations look like this:
$\frac{dy}{dx}=g(x)$ Usually an initial condition (or conditions) will also be provided -- so that the solution ($y(x)$) has value $y=y_0$ at $x=x_0$.
- Our job then is to find the function $y(x)$ which
satisfies both of those conditions.
- Examples:
- Two-percent of the women in a population (half men
and women) give birth each year (assume single
births). Hence, in the absence of deaths or migration,
$\frac{dP(t)}{dt}=.02P(t)$
Do we know a function which is its own derivative? Yes: 0! But that's not the answer (although you see that the differential equation is satisfied for that).
It turns out that exponential functions are proportional to their own derivatives, and so populations tend to grow exponentially in the absence of deaths (or other constraints).
In this case, $P(t)=P_0e^{.02t}$, where $P_0$ is the initial population, and $e \approx 2.718$ is arguably the most important constant in calculus.
- A spring satisfies Hooke's law:
$F=-kx$ That is, the restorative force $F$ is proportional to the displacement $x$ from its equilibrium position. Proportionality constant $k$ is positive, so the negative sign says that the force is in the direction opposite the displacement (that's why the force is called "restorative" -- it seeks to restore the spring to equilibrium).
Newton said that
$F=ma$ "Force equals mass times acceleration".
The acceleration $a$ is the second derivative of $x$ with respect to time $t$. If we put that all together for the spring, we get
$\frac{d^2x}{dt^2}=-\frac{k}{m}x$ For initial conditions, we should give initial position and initial velocity.
"Do I know a function whose derivative(s) make this true?" - The acceleration due to gravity is essentially constant at the
Earth's surface: we can use a differential equation to deduce the
formula for the height $h(t)$ of an object as a function of time $t$:
$g=9.81m/s^2$ Thus, near the surface of the Earth, we get
$\frac{d^2h}{dt^2}=-g$ Once again, we should give initial position and initial velocity.
"Do I know a function whose derivative(s) make this true?"
- Two-percent of the women in a population (half men
and women) give birth each year (assume single
births). Hence, in the absence of deaths or migration,
- A differential equation is an equation linking a function and its derivative(s).
- This process turns out to be crucial for deciding what $f$ looks
like, given $f'$. Remember when we were looking at a graph of $f'$, and
trying to guess what $f$ looks like? Well, we're not going to need to
do that, once we know how to find anti-derivatives. We may find them
analytically, or we may find them numerically -- but we can generally
find one, one way or the other!
- Some examples:
- #3, p. 273 (find ALL anti-derivatives -- the anti-derivative of a sum is the sum of the anti-derivatives)
- #20 (find THE specific anti-derivative)
- #33 (anti-differentiate twice! First find the derivative, then $f$.)
- #41 (find THE specific anti-derivative of $2x+1$ passing through (1,6), and evaluate it at x=2)
- #70
It's time, however, to go back to the dashboard: we're not focused on finding speeds from changes in distance now, but rather we're going to focus on the odometer: how do tell how far we've travelled given a history of our speeds? Back to Day02:
The big ideas of Calc I are contained in Gil Strang's "Auto Analogy": he says that the "The central question of calculus is the relation between [speed and distance traveled]."
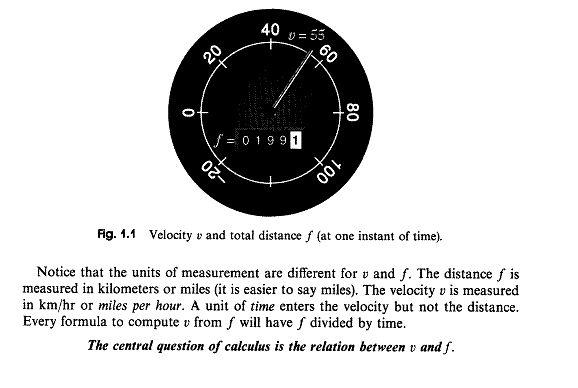
Imagine that the car is operated on a long, straight road. (Just for the sake of convenience, we won't allow it to travel in reverse! Otherwise we'd be talking about velocity -- speed and direction -- rather than just speed.)
- Suppose that you clock your speed
at each minute along a trip, in mph:
minute 0 1 2 3 4 5 6 7 8 9 10 speed (mph) 0 30 45 30 70 65 70 70 45 30 35 Estimate the distance travelled.
- Use Dirt!
- If you were going at a constant rate of speed, you could use the ol' dirt formula: $d=r*t$
- We could imagine that for each short time segment, the given speed
is fixed. This leads to a discontinuous speed function. But
it's easy to calculate the total distance: it's just a bunch of
mini dirt calculations.
- Alternatively, we might fit straight line segments between data
points: this gives rise to the so-called "Trapezoidal
rule". Then we'd have a continuous speed function.
- One thing for sure: since we're dealing with sampled data, we're probably wrong -- we hope that we're close.
- If you were going at a constant rate of speed, you could use the ol' dirt formula: $d=r*t$
- There are several useful rectangular rules, such as
Left/Right/Midpoint rules:
- Estimates for the given data:
- RRR (Right Rectangle Rule): d = 45.5*10 mph*minutes = 7.58 miles
- LRR (Left Rectangle Rule): d = 49*10 mph*minutes = 8.17 miles
- Trapezoidal rule = 47.25*10 mph*minutes = 7.88 miles
- Notes:
-
- Whenever you have two estimates, you have a third:
- the trapezoidal rule is the average of left and right rectangle rules.
- Each of these estimates corresponds to computing a rectangle height (an
average speed), and then multiplying by the total time (10
minutes). Hence we're using the "dirt" formula, and computing the
average (the "area under the curve", even though there's no curve!) in
several different ways.
- Basically, every function can be used to create a table like this, and
then we can use these strategies.
- Example:
- Often (as in the table above) we have data located at equal intervals ($\Delta{x}$). When you have a curve (or a formula) for $f$, you can take the time
intervals shorter and shorter, until you get as close to the area as you
need:
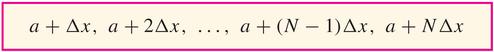
(notice that $a+N\Delta{x=b}$ that is, that $\Delta{x}=\frac{b-a}{N}$)
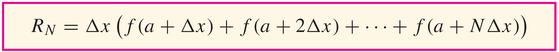
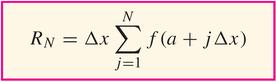
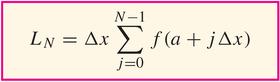
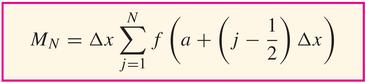
Then, in fact,

- Examples:
- #1, p. 293
- Generalizations?
- The area can be calculated by finding an average value on the
interval, times the length of the interval:
Area under the graph of $f$ from $a$ to $b$ = $\bar{f}(b-a)$ where by $\bar{f}\mbox{}$ we mean an average value of $f$.
- The area can be calculated by chopping the interval $[a,b]$
up into smaller and smaller chunks, and then using rectangular approximations
to the small areas.
- In our work so far, the intervals into which the interval is chopped have been equal-sized: no reason to stick with that.
- If the size of the intervals goes to zero, then the approximations get better and better, until they're perfect!
- The area can be calculated by finding an average value on the
interval, times the length of the interval:
- Some more examples:
- #6
- #15