- A reminder to put your phones away, please.
- I've given you a little assignment (due next Wednesday): I want you to compute a regression equation by hand for the Keeling data. It's just a good exercise to make sure that our equations work (that we'll finish deriving today).
- Also a reminder that your mini-projects #1 are due in a week (next Friday). By the end of the today you should have all that you need to create a linear regression model. Remember that this is a group project, and I just want one report per group. These reports will be made available to all, because we're going to next assemble all the towns into one single model for all of Togo. So I'll need an electronic copy to post.
- We used Mathematica to find linear
models that fit Stewart's Keeling data (that
included a quadratic model, which was linear in its
parameters;
Connor received a gold start for asking about when to stop our modeling: why not consider a cubic, or a quartic, or a quintic, or....
We tried a cubic with the Keeling data, and checked the confidence interval for the cubic term, and it was significant at the 95% level. Interesting!
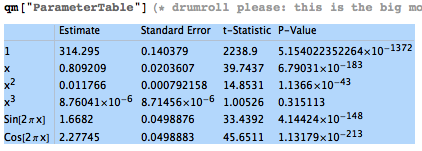
We should realize, however, that we're only looking at bi-annual averages over some smallish part of the Keeling data. When I went back to my office, I used the entire Keeling data set, and this is the result of the Mathematica command "ParameterTable" (which gives t-statistics and P-values, rather than confidence intervals -- I hope that you're comfortable with both!):
- We started to "do the math", to see how to find the parameters $a$ and $b$ of the model $y=a+bx$ that minimize the sum of the squared residuals, using (multivariate) calculus. Let's finish that.
- Then we'll check the results using Mathematica, to see that we get the same fit to Stewart's Keeling data.
- "The
IPCC stands by its equation of 450 ppm = 2 degrees C [of warming]...."
- An extract from Curve Fitting via the
Criterion of Least Squares, by John Alexander. A
bit old-fashioned, but it's got all the major ideas,
and some nice examples.
Alexander also illustrates that one cannot simply invert the regression equation $y=a+bx$ to get the regression equation $x=\frac{y-a}{b}$. So it really matters in linear regression which variable is considered "independent" and which is considered "dependent".
- My multivariate derivation.