
The probability density of a t-distribution looks roughly normal, i.e. bell-shaped (a little shorter and fatter, depending on the number of "degrees of freedom").
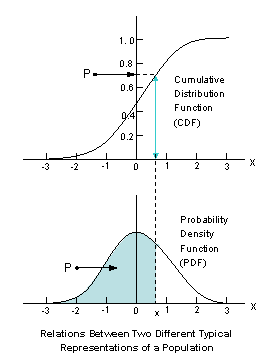
The CDF (Cumulative Distribution Function) is the integral of the density, giving the total accumulated probability: \[ CDF(x)=\int_{\infty}^x \rho(t)dt \]
To find a two-sided "critical value of t" for $1-\alpha$ confidence intervals, we look for where the CDF is equal to $1-\frac{\alpha}{2}$: find $x$ such that \[ CDF(x^{crit})=\int_{\infty}^{x^{crit}} \rho(t)dt = 1-\frac{\alpha}{2} \] So if we want 95% confidence intervals, this is .975. Since the t-distribution is symmetric, I could just as well solve for the negative value, where \[ CDF(-x^{crit})=\int_{\infty}^{-x^{crit}} \rho(t)dt = \frac{\alpha}{2} \]

If the degrees of freedom is small, then the t-distribution will look a little shorter and fatter than a normal.
Confidence intervals for a parameter are computed using the standard errors of the parameters as well, \[ SE=Sqrt(Diagonal(MSE*(X^TX)^{-1})) \] Then, if the confidence required is $1-\alpha$, then the appropriate confidence interval is \[ [\beta_i - t^{crit}_{\frac{\alpha}{2},\nu=n-p} SE_i,\beta_i + t^{crit}_{\frac{\alpha}{2},\nu=n-p} SE_i] \] where $t^{crit}$ is obtained from a t-table, or software (usually).
We've got our estimate in a box, and with confidence $1-\alpha$ the true value of the parameter is inside that box (which also means that with probability $\alpha$ it's outside that box!).