- Roll
- Reminder: please keep the phones out of sight and sound.
- The Cross Country report has been received, and caused
quite a ruckus at my brother and nephew's home.
Said Thad: "Yeehah! Cue the Rocky theme song!"
"I'm justified in claiming my GOATness for all time, lucky underwear and nursing home choice notwithstanding.
Furthermore, "The data was fun, but the analysis comments were even better. Glad that a brief mention of time comparisons led to a real life application for your class. Please pass on my thanks.
"Too fun."
From Thomas: only silence....:(
- Reminder: You have a homework assignment to
hand in today.
- Your next assignment (a group assignment) to turn in is
due Friday.
- For today, I asked you to read the Bestiary of functions paper. We won't really discuss that today, except perhaps in passing. But you want to learn to recognize these broad classes of functions -- and the sooner the better!
- We broke into groups to discuss Dave's stick. What is it, and how
are the marking made?
Comments, questions, concerns?
- Examples of problems and models: Model Classes -- the function zoo
- The Basic Problem
- Linear functions are arguably the most important in
mathematics. At the beginning of a semester I have my
calculus classes (e.g. mat129) take an exam that is
(somewhat) predictive of their chance of success in
calculus:
$grade(K)=3.1K + 27.3$ Final
Course
Grade
(%)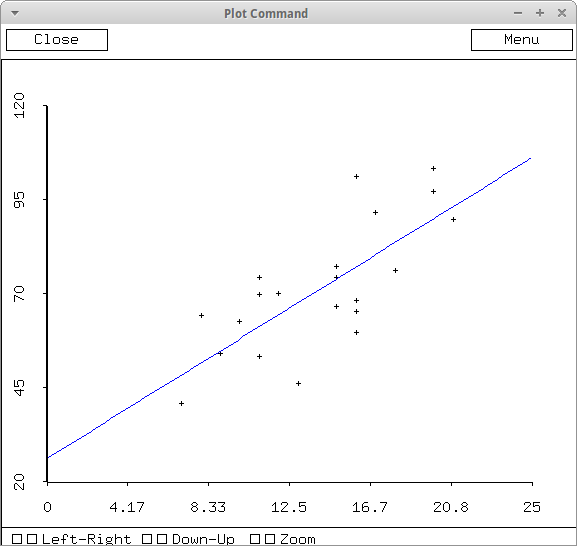
KEMTP score $K$ - Let's talk about whether straight line models -- the simplest
models -- are appropriate, and look at a couple of examples.
In particular, I want to emphasize one of my favorite aphorisms: don't fit a banana with a straight line. That is, if your model is missing something important (e.g. concavity in a set of data), then fix the model!
First of all, regarding straight line models: The Basic Problem document asks "Have you ever read an article in Scientific American, Physics Today, Science or other periodical, and come across a picture like this one...." (a linear regression).
So my most recent edition of Science appeared, and I've flagged all the linear regressions in the Research Section that I found (there are several examples).
- Let's continue by looking at a few "misadventures in modeling":
- James Stewart's Calculus, p. 25: your introduction
to the Keeling CO2 data. What would you see
in the residuals (that is, the difference
between the data and the model)? Stewart describes
interpolation, extrapolation, and the
dangers of his model (p. 27).
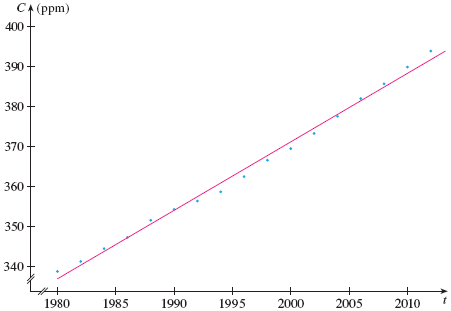
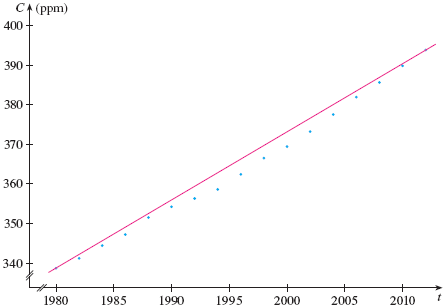
"We therefore predict that the CO2 level will exceed 420 ppm by the year 2029. This prediction is risky because it involves a time quite remote from our observations. In fact, we see from Figure 6 that the trend has been for CO2 levels to increase rather more rapidly in recent years, so the level might exceed 420 ppm well before 2029.
- Here's another example (Mooney and Swift, p. 171): A
modeling misadventure with Advertising Expenditures.
- Here's another example: A
modeling misadventure with corn seedlings.
- James Stewart's Calculus, p. 25: your introduction
to the Keeling CO2 data. What would you see
in the residuals (that is, the difference
between the data and the model)? Stewart describes
interpolation, extrapolation, and the
dangers of his model (p. 27).
- So we might consider a "modified" Basic Problem: to find a
function that fits the data (whether a straight line or
not). For that it is good to have a healthy stable of functions
to choose from, many of which are illustrated in the Bestiary of functions,
from Ben Bolker's Ecological Models and Data in R.
I asked you to read this because straight lines are not enough: we need a variety of functions, for a variety of situations. For example, Riegel thought a power function would be nice. I thought that Ben's comment on the first page was funny: "If you begin to feel bogged down you can skip ahead and use the section for reference as needed." (I can see why one could get bogged down!)
If you did get bogged down, then I hope that you at least had a look at the pictures, on pages 123, 124, 128, 132!

- Now we want to see how to use Mathematica to perform linear
regression in the case of Stewart's version of the Keeling
CO2 data.
We will use this Mathematica code to find "linear" models that fit Stewart's Keeling data (that included a quadratic model, which was linear in its parameters (more on that as we derive the equations next time).
I'll walk you through this -- especially important if you're new to Mathematica.
- Then you might modify things a bit to do some linear regression on the data for Dave's stick....
- The Basic Problem
- "The IPCC stands by its equation of 450 ppm = 2 degrees C [of warming]....": For years scientists have said that if atmospheric levels of carbon dioxide reach 450 parts per million (ppm) the planet would heat up by an average of 2 degrees Celsius above pre-industrial levels. They have also said that if the world crosses that threshold, ecosystems worldwide would suffer serious damage.