The equations of the "Basic Model" are:
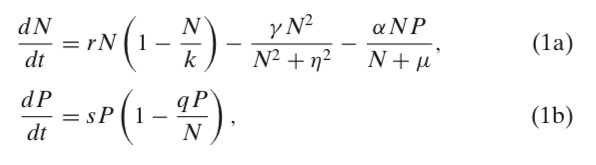
This is obviously a little more complicated than the Lotka-Volterra system -- and no doubt a little better representation of the biological world. The authors ultimately incorporate three populations of predators into the system (those poor hare! Everyone seems to find them delicious...:). So their "Full model" looks like this, where the index $i$ represents the $i^{th}$ predator population:
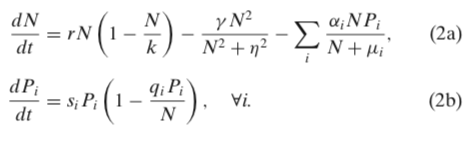
So for the full model, there are actually four equations (one for the Hare $N$, and three for $i=\{lynx,owl,coyote\}$).
We'll be focused only on the Lynx, however; so we'll be dealing only with the basic model, where $N$ represents the Hare, and $P$ represents the Lynx.
In this lab you'll be creating a Word doc (or similar) to illustrate that you've carried out the steps in this lab. So you might open that up.
Now let's get started....
- Open the article from the link above.
On page 98 you will read the description of how the Basic Model was constructed. Consider the following parameter and population choices:
initial hare population $x_0=1.7$ initial lynx population $y_0=1.7/q$
(where $q$ is given below)carrying capacity $K=1.75$ Hare birth rate $r=8$ Hare generalist predation rate $\gamma=0.035$ Generalist equation term $\eta=1.25$ Hare specialist predation rate $\alpha=1867$ Specialist equation term $\mu=0.3$ Lynx L per H conversion rate $q=212$ Lynx birth rate $s=0.85$ Graph each of the four terms on the right hand side of the equations, \[ r N \left(1 - \frac{N}{K}\right) \\ - \frac{\gamma N^2}{N^2 + \eta^2}\\ - \frac{\alpha N P}{N + \mu}\\ s P \left(1 - \frac{qP}{N}\right) \] using those parameter values above. Graph the first three as functions of $N$, and the fourth as a function of $P$ -- on the interval $[0,2K]$ in the case of the hare, and on the interval $[0,2K/q]$ for the RHS of the lynx equation. Use the constant initial value of $P$ when graphing functions of $N$; and vice versa for the function of $P$.
Each of these represents some contribution to the rate of change of these populations: positive rates of change mean population growth; negative rates of change mean population loss.
Paste the graphs into your document.
Succinctly explain the behavior and impact of each of the four parts of the equations, in your own words, and relate your discussion to the graphs.
-
Visit my
Tyson Basic Model Insight. "Clone
Insight" yourself, so that you have a copy.
The first things I want you to do is read the information on this system that I have written in the insight model itself. It explains, in brief, some of what I explain below.
The teachable moment:
That initial value for $P$ was a little weird. In the following, you'll see why I wrote it the way I did.
The basic model system should be re-written because it has more parameters than really needed. In particular, we can combine two parameters into one: $\alpha$ and $q$ are converted into one ratio ("alphaQratio") in the following (and here I am using Tyson's notation): \[ \frac{dN}{dt}= r N \left(1 - \frac{N}{K}\right) - \frac{\gamma N^2}{N^2 + \eta^2} - \frac{\alpha N P}{N + \mu}\\ \frac{dP}{dt}= s P \left(1 - \frac{qP}{N}\right) \] Multiplying through the predator equation gives \[ \frac{d(qP)}{dt}= s (qP) \left(1 - \frac{(qP)}{N}\right) \] so a simple change of variable yields \[ \frac{dw}{dt}= s w \left(1 - \frac{w}{N}\right) \] And since we've exchanged $P$ for $w=qP$, we need to replace $P$ in the first equation: \[ \frac{dN}{dt}= r N \left(1 - \frac{N}{K}\right) - \frac{\gamma N^2}{N^2 + \eta^2} - \frac{\alpha N \frac{w}{q}}{N + \mu} = r N \left(1 - \frac{N}{K}\right) - \frac{\gamma N^2}{N^2 + \eta^2} - \frac{\frac{\alpha}{q} N w}{N + \mu} \]
so that the new system becomes
\[ \frac{dN}{dt}= r N \left(1 - \frac{N}{K}\right) - \frac{\gamma N^2}{N^2 + \eta^2} - \frac{\frac{\alpha}{q} N w}{N + \mu}\\ \frac{dw}{dt}= s w \left(1 - \frac{w}{N}\right) \] (and notice that $\alpha$ and $q$ only appear once, together, as a ratio -- so we could define a new parameter, alphaQratio, that controls the dynamics.) This is what I do in the InsightMaker model you're going to consider.
This is a nice change of variables, because $w=qP$ is roughly the same size as $N$ -- since $q$ is roughly the number of hares per lynx in an equilibrium population. So the two variables are roughly the same size. It makes graphing easier, for one thing, and may make numerical solutions behave better.
Have you ever seen a piece of equipment where you turn the wheels (steer) using two separate levers, one for each hand? One could drive a car that way, but we prefer to use a steering wheel (which you can operate one-handed). Two versus one -- so long as we accomplish the same thing -- turning the car the way we want -- we reduce the complexity with only one parameter.
In this lab, you will interact with your InsightMaker model.
- Now to the InsightMaker stuff that you're going to report back to me:
For "Settings", make sure that you're running in Years, 0 to 28, with RK4, and with Simulation Time Step of 0.1; and verify that you're using the parameters and initial values listed above (I've changed a few of them, perhaps... And note that I've replace $P$ by $w=qP$ in the InsightMaker model -- so the initial value of $w$, $w_0$, is 1.7).
-
Hit "Simulate" once you've confirmed that everything is as it should
be. Describe what's happening with the populations -- how do they
vary? Which one is leading, and which is following? Tell the story.
What do you think happens as time $t \to \infty$?
Make copies of both plots -- the population time series, and the phase portrait to include in your Word Doc. Again, you can use the slider along the bottom to see how the system is evolving over time.
- Now change $\alpha$ to 505 in the ratio alphaQratio. What happens
this time when you simulate? What do you think happens asymptotically
(as time $t \to \infty$)? Include images.
- Now return $\alpha$ to 1867.0 in the ratio alphaQratio,
and change $s$ to 1.5. What happens this time when you
simulate? What do you think happens asymptotically (as time $t
\to \infty$)? Include images.
- Now it's challenge time: two challenges. Find starting values for
the populations so that the cycles start small, and get bigger;
and so that the system approaches a limit cycle (which is the sort of
thing we expect biologically). You may also alter other
parameters. Report your parameter choices, and show a graph of the
population time series.
- Second challenge: find starting values so that your solutions
look qualitatively like those waves of the hare and lynx of
Figure 2, p. 102. Show a graph, and report parameter
values. (I think that there's more of a "forward lean" to the
solutions than you see in our initial graph.)
Remember that the authors have scaled their population to 0 to 1, so that they can plot them together (see the caption to Figure 2).
This is fundamentally the goal of the authors -- they seek to match oscillations in real data with their models. We'll do something easier here: try to match the oscillations in their model with oscillations from the same model! (Important Note -- the parameter values given in the paper don't work, which I found out early when I was trying to replicate their work. So I had to hunt around to find parameter values that would give the cycles they illustrated.
Stuff happens....).
-
Hit "Simulate" once you've confirmed that everything is as it should
be. Describe what's happening with the populations -- how do they
vary? Which one is leading, and which is following? Tell the story.
What do you think happens as time $t \to \infty$?
Links: