Once again we will start with an SIR model -- Susceptible, Infected, Recovered -- but will now introduce death.
Now let's get started....
- Visit our
SIR model that includes death. You'll want to"Clone Insight".
- Recall that an SIR model is a system of differential equations
(three of them, to be precise), the simplest of which looks like this:
\[ \frac{dS}{dt} = -\alpha S I\\ \frac{dI}{dt} = \alpha S I - \beta I\\ \frac{dR}{dt} = \beta I \]
This simple SIR model generally assumes that
- The disease is short-lived and non-fatal.
- The disease is spread by contact between individuals.
- The individuals who recover develop immunity.
These equations give the rates of change of the four populations. But, since the total never changes (no birth), we just reshuffle the populations over time; and we must have a constant total population $N(t)=S(t)+I(t)+R(t)+D(t)$.
- Pull up the
MAA website wherein they describe a simple SIR model. You might
want to read over their description of the SIR model. I think that they
do a very nice job of laying out the situation -- summarizing what we
covered in the first lab.
We'll begin by reproducing their results. A couple of things:
- They had a population of 8 million, and a starting population of 10 individuals. We have a starting population of 100. So we scale the starting value of the population of infecteds to \[ I_0=(100/8000000)*10 = 1.25{\textrm{E-4}} = 0.000125 \]
- Their model contains no death. So some of our "flows" are not flowing...:)
$S(0)=S_0$ $100-0.000125$ $I(0)=I_0$ $0.000125$ $R(0)=R_0$ $0$ $D(0)=D_0$ $0$ $\alpha$ $0.5$ $\beta$ $0.33333$ $\delta$ $0.0$ Notice once again that I've written the initial populations so that their sum, the total population, is 100. So we can interpret the populations as the percentage of the total population.
Notice also that you can set your rates with the sliders on the right, under the Insight information.
Set your time setting for days, 0 to 150; RK-4, with step-size of .1.
So here's their story:
"For this particular virus -- Hong Kong flu in New York City in the late 1960's -- hardly anyone was immune at the beginning of the epidemic, so almost everyone was susceptible. We will assume that there was a trace level of infection in the population, say, 10 people. Thus, our initial values for the population variables are $S(0)=8,000,000$, $I(0)=10$, and $R(0)=D(0)=0$."
Simulate, using the parameters specified in the table above (adjusted to correspond to theirs).
- Include your graph of populations versus time. It should look pretty much like that in the MAA article.
- Describe what has happened, in terms of the three populations, as $t$ runs from 0 to 150 day.
- What happens as $t \to \infty$? Why does this make sense?
- Flattening the curve:
We've all heard a lot about the notion of "Flattening the curve". The article Flatten the COVID-19 curve suggests a strategy for "flattening the curve" of the infected population. Here's their objective:
"Current discussions about interventions for the ongoing COVID-19 outbreak talk a lot about flattening the epidemic curve, i.e. to slow down the outbreak dynamics. Because of limited health capacities, stretching out the outbreak over a longer time period will ensure, that a larger proportion of those in need of hospital treatment will actually get it. Other advantages of this approach are to win time in order to find better treatment forms and, possibly, to eventually develop a vaccine."
However they point out something important: "Reducing the basic reproduction number by drastically reducing contacts or quickly isolating infectious diseases also reduces the size of the outbreak. Also others, like Ben Bolker have pointed out this flaw." (I thought that is was interesting that our old friend Ben Bolker figure in here, he of the Bestiary of Functions...).
Their picture of the idea is here: we're going to cut the infectivity rate for a time, via social distancing:
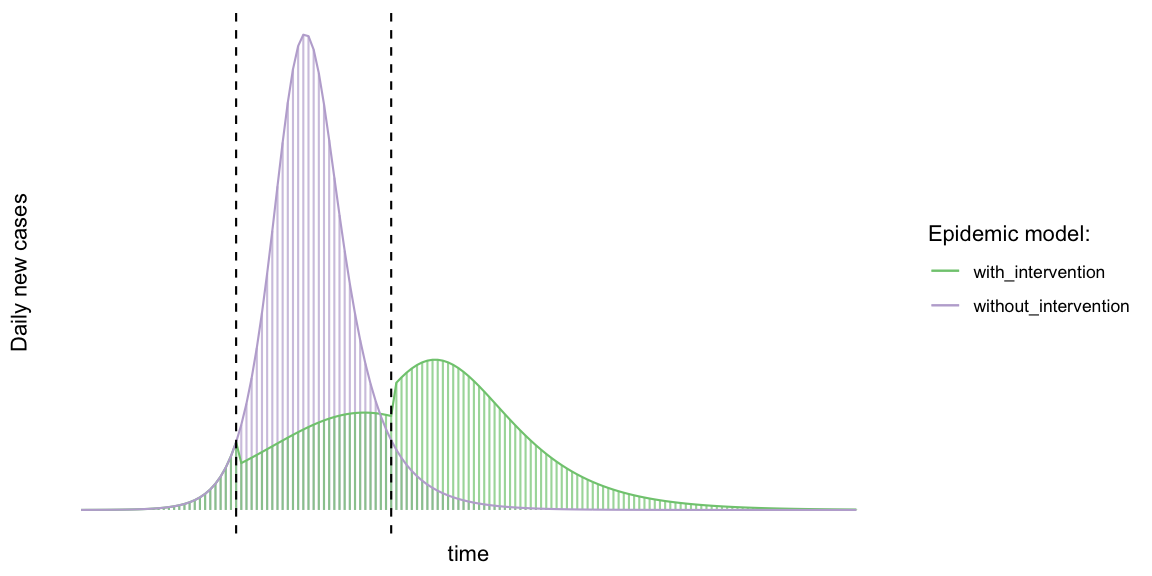
The author's suggest one strategy, which is to reduce the infectivity, by social distancing. And they suggest that we create a "step-function" to carry that out in our model. Check your initial settings:$S(0)=S_0$ $100-0.001$ $I(0)=I_0$ $0.001$ $R(0)=R_0$ $0$ $D(0)=D_0$ $0$ $\alpha$ $0.45$ $\beta$ $0.2$ $\delta$ $0.0$ Simulate, and report. Keep your plot open, so that we can compare to what is to come.
Verify that your results look approximately like their plot "without interventions" (but notice that they're plotting new cases only -- whereas we're plotting all infecteds).
$Note$: To focus on infecteds, your can click on the dots in the legend for recovered and susceptible populations, and they won't be shown (bringing the infecteds into focus).
- Now we're going to intervene, and see if we can cut down the peak
that caused so much trouble for our medical system (flatten the curve).
In Insightmaker, we can implement "social distancing from 30 days to 110 days by replacing the value of $\alpha=0.45$ with the following step-function:
IfThenElse(Time() < {30 days}, 0.45, IfThenElse(Time() < {110 days}, .3,.45)) It basically says that infectivity declines for awhile (because we're social distancing, say): \[ \alpha=\left\{ \begin{array}{cc} {0.45} & {t<30}\cr {0.30} & {30 \le t < 110}\cr {0.45} & {t \ge 110}\cr \end{array} \right. \]
Change $\alpha$ to this step function, then focus in on the infected, and illustrated (and describe) what has changed).
Use "Tools", "Compare results", to compare the infecteds from the two simulations.
Then drop the social distancing to just a month or so, i.e.
IfThenElse(Time() < {30 days}, 0.45, IfThenElse(Time() < {60 days}, .3,.45)) Simulate, and compare infected populations in all three simulations.
Explain what happened.
- Now we'll add a little death. Set $\delta=.005$. We might think of
that as meaning that 1/200 of the infected die each day.
Create graphs using successively more vigorous social distancing (why does this succession of $\alpha$ values represent more vigorous social distancing?). Set your time setting for days from 0 to 250. \[ \begin{array}{|c|c|} \hline {\alpha} & {0.45}\cr \hline {\alpha} & {IfThenElse(Time() < \{30\ days\}, 0.45, IfThenElse(Time() < \{60\ days\}, .3,.45))}\cr \hline {\alpha} & {IfThenElse(Time() < \{30\ days\}, 0.45, IfThenElse(Time() < \{110\ days\}, .3,.45))}\cr \hline {\alpha} & {IfThenElse(Time() < \{30\ days\}, 0.45, IfThenElse(Time() < \{110\ days\}, .1,.45))}\cr \hline \end{array} \]
Do a "Tools", "Compare results" with the dead population. How much difference do these choices make in deaths in the population? The last one might surprise you....
- Finally let's make a change in the death rate. Rather than being a
fixed constant of the infected population, it seems that, should the
infected population become too high, the hospital systems will be
overwhelmed, and the death rate will skyrocket. Hence it makes sense to
make $\delta$ a function of the infected population. So create a link
from the infected population to the death rate $\delta$, and set
\[
\delta=.005*\left(1+\frac{3 I}{5+I}\right)
\]
For the same four scenarios, \[ \begin{array}{|c|c|} \hline {\alpha} & {0.45}\cr \hline {\alpha} & {IfThenElse(Time() < \{30\ days\}, 0.45, IfThenElse(Time() < \{60\ days\}, .3,.45))}\cr \hline {\alpha} & {IfThenElse(Time() < \{30\ days\}, 0.45, IfThenElse(Time() < \{110\ days\}, .3,.45))}\cr \hline {\alpha} & {IfThenElse(Time() < \{30\ days\}, 0.45, IfThenElse(Time() < \{110\ days\}, .1,.45))}\cr \hline \end{array} \] Compare the resulting dead populations. What policy recommendations could you make to your government?