- The exams are still being graded, but should be finished by
tonight. Your scores will be averaged (just average the
percentages from your IMath and your Canvas parts). Your
IMath score may be given as total points; to get a percentage,
divide your total score by 1.20.
- As we move forward we're going to be tying up a few loose ends;
but in tying up those ends, we're going to be pointing to a few
of the topics we have in our future.
- While we do have one more civilization and their numbers
to study (the Egyptians), we will be moving along to
the discussion of more "visual" mathematics. I read a
story today in the Guardian, about the science behind
Salvador Dali's works (such as The Sacrament of the
Last Supper):

This work features one of the topics we'll be studying down the road -- the Platonic solids. But it is also famously regarded as a painting in which the artist made conscious use of the golden ratio, which we cover today. This rectangle is almost "golden" -- the most beautiful rectangle, according to some of the ancient Greeks.
- Here's a video covering today's material.
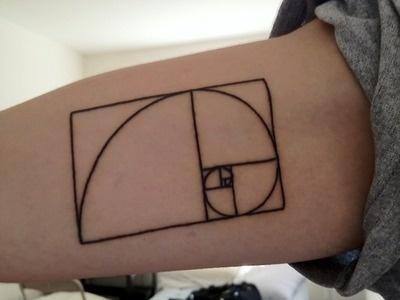
- We will discover that the Fibonacci spiral leads to rectangles
that tend toward a common side ratio of about 1.618.... The
"Golden Rectangle" as defined by the Greeks has a side ratio of
\[
\varphi=\frac{1+\sqrt{5}}{2} (\approx 1.618)
\]
called the golden ratio.
- As we move toward the so-called "golden mean" and "golden
rectangle", we'll start with a nice Fibonacci spiral (we've done this
already: see this
site for more on these spirals).
We build the Fibonacci spiral by building bigger and bigger rectangles. The shapes of the rectangles change as we go along, in such a way that the ratio of side lengths are Fibonacci numbers. Let's look at the sequence of the ratios....
So let's recap the spiral building process, with a focus on those side ratios.
- Start with a piece of graph paper (the wide way), and darken the square in the 10,10 spot (ten over, ten down). You might want several colors, if you've got them -- might as well make this pretty!
- Rule: attach the largest square you can, in either a clockwise or counter-clockwise fashion, to make a larger rectangle. We'll go counter-clockwise.
- Do it again, do it again, do it again! (You could do it forever....)
- What do you notice about the dimensions of the rectangle? It's the ratio of those dimensions that interests us most -- the ratio of dimensions (larger to smaller) dictates the shape of the rectangle.
- The thing we are approaching is the so-called golden rectangle,
whose side-lengths are in the ratio called "the golden
ratio". But we will derive the golden rectangle in a
different way -- the way that the Greeks did it! When
we're done, we'll have also defined the "golden mean",
or the "golden ratio".
- Begin with a rectangle.
- Remove the largest square possible from the rectangle, to leave a rectangle.
- If the rectangle that results has the same shape as the original rectangle, then that rectangle is golden.
Now if we look back at the Fibonacci spiral sequence of rectangles, we see that they're tending toward a golden rectangle.

Both had roughly the same effect, however.
Each of these as an example of a "fractal process": a simple rule, applied recursively (that is, do it again, and again, and again!). We believe that nature loves fractals, and we'll study them in more detail down the road.
But, before I go, here's an example fractal I just made for my son and his wife, with their forever and infinite friend Bernie Sanders:

And here's another -- A Fibonacci spiral fractal comic I just made, which I have just now entitled "Flirting with Death Spiral". Infinite fun!

You'll be making these, too, soon!
- Now, back to Pascal's triangle. Let's look a little further into
it. In particular, note that Pascal's Triangle contains the
Fibonacci numbers -- but they're hidden. Let's bring them to
light.
- Use the hexagonal paper to create a version of the Pascal triangle.
- Now let's find those Fibonaccis....
- Pascal used "his" triangle to compute probabilities. It turns out
that it's very useful for counting things. Blaise Pascal and Pierre de
Fermat were working on "Number Theory" together.
- Pascal's triangle is useful for counting the ways of
combining terms in the expression
$(a+b)^n$
So, for example,
\[ (a+b)^0=1 \] \[ (a+b)^1=1a+1b \] \[ (a+b)^2=1a^2+2ab+1b^2 \] \[ (a+b)^3=1a^3+3a^2b+3ab^2+1b^3 \]
(please see your assigned reading).
I hope that you noticed Pascal's triangle peeking out from the right hand sides above!