- Today we continue with one of my favorite topics: Fractals!
Fractals tend to be very popular for creating logos, as are knots. I hope that you're going to like making some.
- Here are some videos covering today's material.
- The concept of fractals is the most modern mathematics that we
study in this course. We've worked our way up from the Babylonians all
the way to the 21st century.
- Here is our "intuitive" definition of a Fractal:
-
A world within a world! By which I mean that there's a perfect copy of the fractal contained within itself -- and perhaps infinitely many!
For example, in the A0 Fractal, the whole rectangle (A0 paper) contains smaller (but perfect) copies of itself -- A1, A2, A3, .... papers.
- We began by talking about some of the fractals we've known: the Fibonacci rabbit tree is fractal, as is the Golden rectangle.
- Some examples you might have seen before:


- We saw how one can create new fractals with rectangles (e.g. the A0 paper fractal)
- We talked about line fractals (where the initiator is a stick) and area fractals (where the initiator is a two-dimensional object).
- We saw and created the classic Koch fractal (a stick fractal)
- We also created an area fractal, based on triangles, called Sierpinski's triangle. Sierpinski's triangle is "infinitely deep".... (You need to listen to the Doors, or Jefferson Airplane, or Jimi Hendrix while studying fractals.)
In each case, there's "a world within a world": that's the most important property of fractals.
- Today we'll start by having a look at a recent (January, 2015) addition to the fractal family: the
Harriss fractal). It starts with the golden rectangle, and then makes a slight change.
- I've found a Java program (from here)
that we can use to visualize fractals using what is known as
the "L-System" (Lindenmayer Substitution Fractals).
- a simple rule
- repeated over and over and over.... but
- simple rules, intense content! Fantastic creations are a snap.
- The Koch fractal is this:
- Axiom: f
- Rules: f=f+f--f+f
- Start Angle: 90
- Turn Angle: 60
You might try creating some of your own. Hey, I found a better one! This one you can do on-line, without downloading anything.
The Koch fractal is given by (you can copy and paste):
- Axiom: f
- Rule 1: f=f-f++f-f
- Angle: 60
Play around, have fun!
- Now back to Pascal's triangle. What does it have to do with
Sierpinski?
Let me re-introduce you to Vi Hart, who will talk us through the relationship between Pascal and Sierpinski. She talks really fast, however!
Then we'll try her method to see how, within Pascal, there's Sierpinski....
- even plus even is even
- odd plus odd is even
- even plus odd is odd
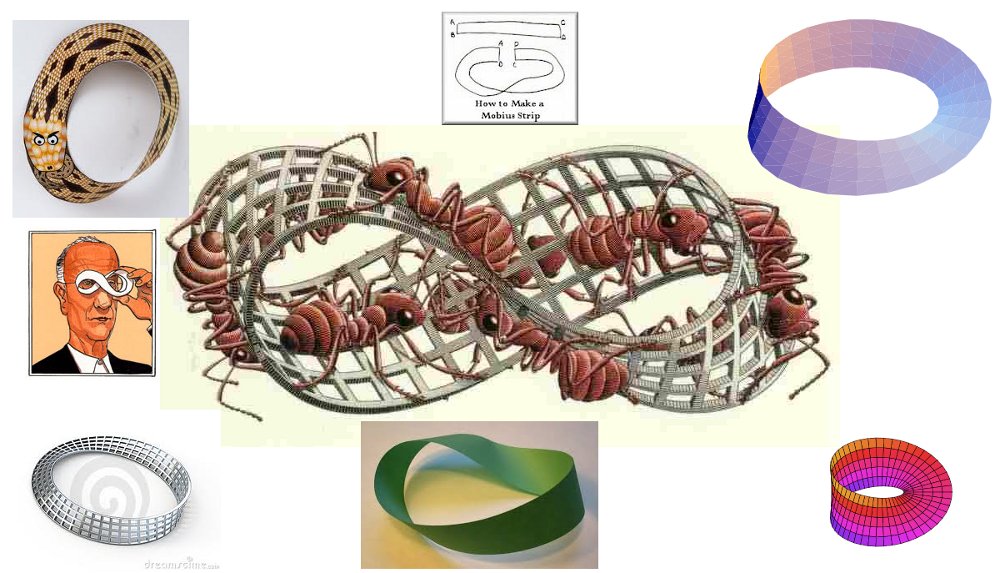
- Finally I want you to create a fractal image, like my image of
"Flirting with Death Spiral" I shared with you last time:

For that you will go to my special pages
- "I'm working on a new series of Platonic solids, to be released as #CryptoArt collectibles.": Joanie Lemercier, a French artist known for his futuristic light sculptures, was one of the first to dig into NFT's environmental consequences. He had just released six tokenized videos, inspired by platonic solids, which were snapped up by buyers. But he had heard of the growing alarm over Bitcoin's energy use, which worried him: Mr. Lemercier has also been involved in climate activism, campaigning for a move away from coal.
- L-Systems
in PostScript, from which I generated this image:

Cantor dust:

star:

koch:

square koch:

four:
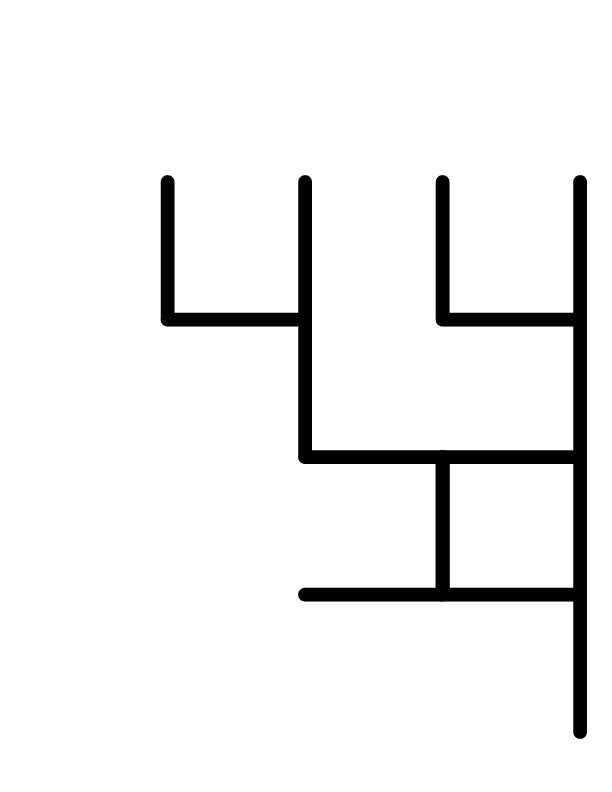
Standard Koch:

Square Koch:

sKoch:
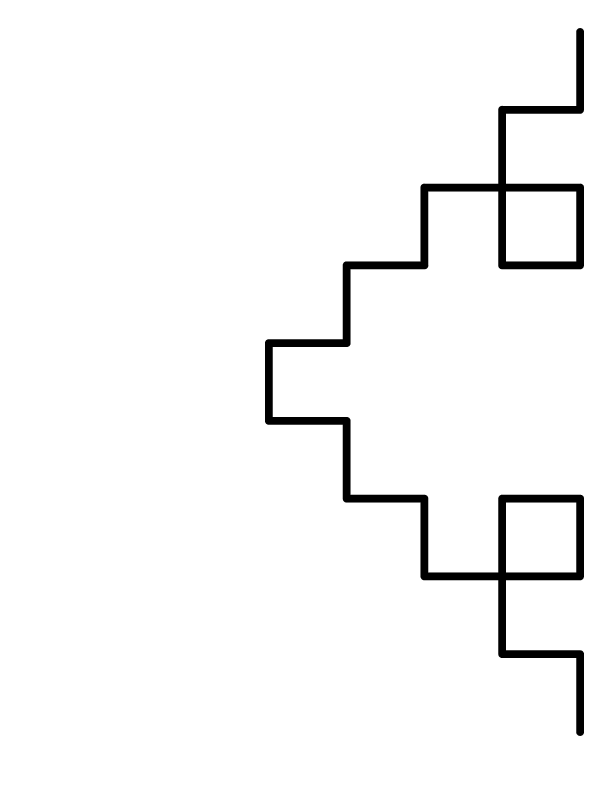
flowSnake:

Sierpinski:

Sierpinski, too:

Here's a "simple dragon":
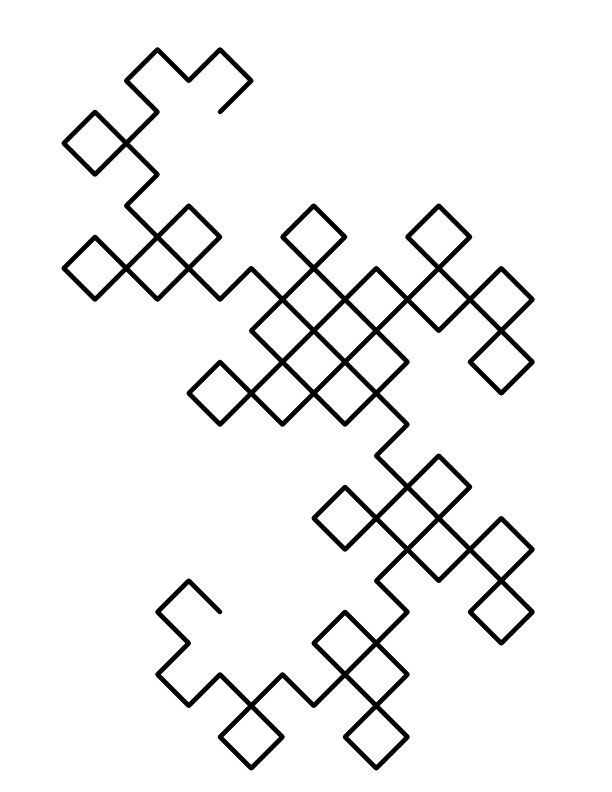
and a lot more complicated dragon, complicated merely by more iterations (more "do it again, do it again"):

Do you see an infinite chain of dragons above?
- I first encountered the L-Systems fractals at britton.disted.camosun.bc.ca/fractals_arcytech/lsystems.html, but that's a dead link. However, I copied the files, and have a local copy here. However, web browsers these days don't seem to like the applet tag in javascript, so this doesn't work anymore in a standard web browser...:(