Day 06, Play-by-Play

Today I'll ask you to pay a visit to the in-class page. It has a lot of the details.
There's a bit of a review of last week's testing material, including another on-line testing tool (which we used to check our breast cancer numbers).
What you on-line folks missed was the very enjoyable discussion of whether six (and numbers, more generally) is discovered or invented by humans.
- Invention was the early favorite. There were comments relating numbers to counting, which seems like a human invention (does nature need to count?).
- There were comments about six being "three + three"; and
- One student mentioned that other creatures are actually able to count (even insects!). So if it were just down to counting, why it's clear that it's not just humans who invented that.
- I suggested that I favored discovery, since nature knows that in CO₂, for example, a carbon knows that it needs two oxygens (not one or three); I also mentioned that the sun "knows" how many planets it has in its orbit, but a student countered that humans invented the notion of planet (by comparison with other satellites), so that's a bad example. I agree!
There was a discussion of the moments in the video where the concept of "one-to-one" came up (more on one-to-one in an upcoming reading).
1. The penguins each put in one order -- six penguins, each a fish. One way to proceed would be to give each penguin a plate, and have each one report to the kitchen, and receive their fish.
  Six fish would go out the door
2. We talked about the blocking. What if all the penguins had said "fish" at once? We'd have no idea how many fish to fix. But we heard "fish, fish, fish"; and then the other three penguins say (off camera) "fish, fish, fish".
  In fact it was the blocking mismatch that allowed Humphrey to know that his friend didn't get the order right; she said
```
				"fish, fish, fish
				 fish, fish" 
		
```
  and that didn't match with the sound in Humphrey's head... with the six fish in his head.
3. But I'd say that the explicit example of one-to-oneness occurred at minute 1:20, when the counting occurred, and each fish was matched with a counting number, from 1 to 6.
  Since we ended on 6, we know that 6 fish (and only 6 fish) are necessary.
So what is six? I argued that one can't understand 6 unless one understands 5, then 4, then 3, then 2, then 1. And, in some way, 6 includes 5, and 4, and 3, and 2, and 1 (and 0! -- but 0 is a strange beast, and we'll talk more about it as we go along).
So we talked about using complete graphs to represent numbers. Here are the counting numbers from 1 to 6:

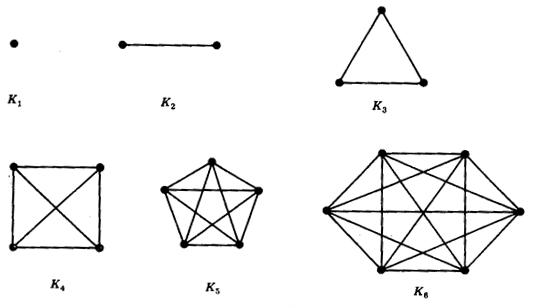
If we think of counting numbers that way, we can see that "two" ($K_2$) contains two copies of "one" ($K_1$); "three" ($K_3$) contains three copies of "two"; etc.
There are six copies of "one" within "six" ($K_6$).
We also discussed how the "bad definition" -- "six is a shortcut for counting by ones -- six times" -- can be fixed up at least a little, using the student's notion that "six is three plus three";

six is a shortcut for counting by ones -- three plus three times
Except that now we need to know what three is (two plus one), and then what two is (one plus one), so we're going to say that

six is a shortcut for counting by a certain number of ones -- one plus one plus one plus one plus one plus one
NOT very satisfying!:)
In the end, a suggestion to Ernie, Humphrey, Ingrid, and the penguins: just send $K_6$ to the kitchen, and match a fish at each vertex!
But interesting question for future discussion: how many edges does each complete graph have? How does the number of edges increase as the number $n$ in $K_n$ increases?

Website maintained by Andy Long. Comments appreciated.