-
- This session will be captured on Zoom, if I remember to turn it on, and record it.
- Our page of zooms and the play-by-plays.
- You have a new IMath assignment, which will be due on Friday,
3/18, of the week following Spring break.
Speaking of Spring break, have a good one! Relax.
- And there's good news following Spring break (this from NKU's
President, RE Covid):
Effective Tuesday, March 8, masks will be optional on campus, with these exceptions:
- Masks are required during class meetings in classrooms and lab spaces, through Monday, March 21.
- Masks are required in NKU Health, Counseling and Student Wellness facilities.
- Masks are required for at least five days following diagnosis of or exposure to COVID-19, per CDC policy.
- Individual employees may continue to require masks in individual private offices where they meet with students, other employees or visitors.
- We began by playing Sherlock Holmes in Babylon, with this artifact (a clay tablet):

Buck says this "Confronted with an artifact from an ancient culture, one asks several questions:
- What is this and what are its properties?
- What was its original purpose?
- What does this tell me about the culture that produced it?
As base 60 people, the Babylonians used powers of 60 to write their numbers. They had 59 digits (because they didn't have the 60th -- 0, my hero!) -- the numbers from 1-59.
We concluded that this is a table of two columns of two columns: integers on the left, and their multiples of 9 on the right. I think that we've got this one down cold.
The Babylonian used places for 60s and 1s, at least (and we suspect that they have a $60^2=3600$ place as well, and so on.
Sadly, they were not acquainted with zero.
- We watched the Schoolhouse Rock video Zero, My Hero.
(favorite lyrics: "et cetera, et cetera; ad infinitum; ad astra1; forever and ever")
So, as we turn to the new world, is there any improvement in the zero situation?
- The mystery of the Mayans....
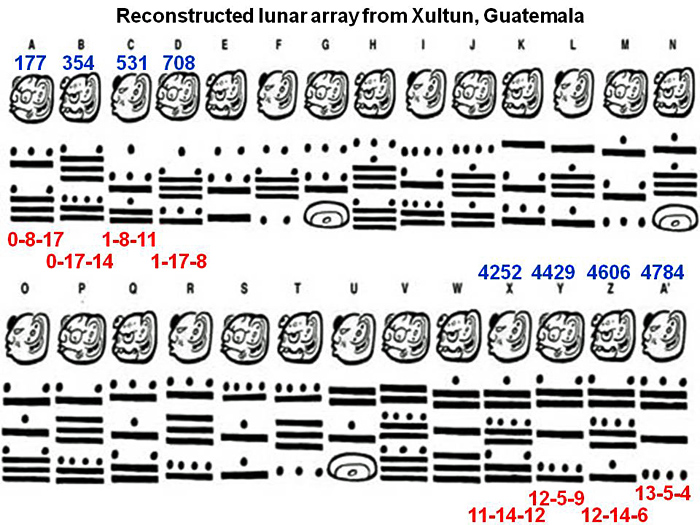
We deduced that
- They had three symbols -- a bar for five, a dot for one,
and... drumroll please,....
- they had a zero! Which looks like a loaf of bread (or is it a
cowry shell?).
- Their base was 20 -- they counted on their fingers and toes.
- They used place value, and their places go from the bottom up!
They have a ones place, and a 20s place; that explains the first entry,
177: $177=17+8*20$.
So we would have expected their places to continue like \[ (20^0, 20^1, 20^2, \ldots)=(1, 20, 400, \ldots) \]
But they don't! Look at the 708 entry.... There is one dot in the next place up. What must its value be?
- Indeed, something unusual happens in the third place. While their
first two places are for the ones, and for the twenties, their third is
360 (oddly enough -- 18*20). Remember that this is a calendar. Why 360?
After that, they resume using powers of 20! So their places are the (1, 20, 360, 7200, etc.): $(20^0, 20^1, 20*18, 20^2*18, 20^3*18, etc.)$
- There's some interesting periodicity in here (Savannah mentioned some of it -- the periodicity in the zero, as well as the slow increase in numbers in the third place).
- They had three symbols -- a bar for five, a dot for one,
and... drumroll please,....
- Are there any other mysteries to clear up, or that you can clear
up? I warned about not following patterns too quickly -- you might have
deduced that there's 177 days between each of the numbers at the top;
you're right for awhile, until you're not!
Do you see how this 177 explains Savannah's observation about the third place?
Think about making change, and just using strange bills: for the Babylonians, you use
- How would the Babylonians write these numbers:
- 47
- 573
- 1,60, and 3600
- How would the Mayans write these numbers:
- 47
- 573
- 3600
- 14001