-
- This session will be captured on Zoom, if I remember to turn it on, and record it.
- Our page of zooms and the play-by-plays.
- You have a new assignment: a
reading regarding symmetry, and some assigned exercises from
that reading (due Wednesday, 4/6).
Plus an article from the New York Times, which describes why geometry is our special human superpower....
- I pushed back the due date on your IMath assignment, due Monday
(4/4), which will check to see if you're able to win at
Fibonacci Nim.
There are also some throwback questions, to make sure that you're getting ready for our next exam (not this Friday, but the following Friday, 4/8).
An Euler example:

Keep going:
What's the fewest number of doors you could close (or add!) that would make possible
- an Euler path?
- an Euler circuit?
- More on that third and last great factorization (into Fibonacci
numbers), and how to use the Fibonacci factorization to win at nim.
(By the way: don't call it Fibonacci Nim, because that gives away a secret toward the strategy; just call it "Nim", or "Fraudini Nim"!)
- I read a
story a year or so ago in the Guardian, about the science behind
Salvador Dali's works (such as The Sacrament of the
Last Supper):

This work features one of the topics we'll be studying down the road -- the Platonic solids. But it is also famously regarded as a painting in which the artist made conscious use of the golden ratio, which we cover today. The dimensions of this painting (the rectangular frame) create a (nearly) "golden rectangle" -- the most beautiful rectangle, according to some of the ancient Greeks.
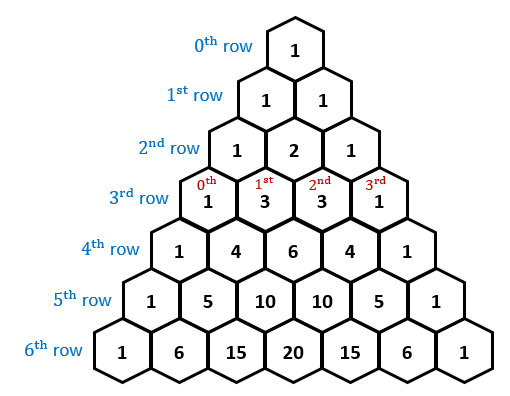
- Before we head there, however, let's go back to Pascal's triangle
for a moment. I want to show you that, in addition to
everything else in there, Pascal's Triangle contains the
Fibonacci numbers! But they're hidden. Let's bring them
to light.
- We'll use the hexagonal paper to create a version of the Pascal triangle.
- Now let's find those Fibonaccis....
- We've made some Fibonacci spirals -- but today we want to make
Golden spirals.
- As we move toward the so-called "golden mean" and "golden
rectangle", we'll start with a nice Fibonacci spiral (we've done this
already: see this
site for more on these spirals).
Ordinarily we build the Fibonacci spiral by building bigger and bigger rectangles. The shapes of the rectangles change as we go along, in such a way that the ratio of side lengths are Fibonacci numbers. Let's look at the sequence of the ratios....
So let's recap the spiral building process, with a focus on those side ratios.
- Start with a piece of graph paper (the wide way), and darken the square in the 10,10 spot (ten from the left, ten down from the top). You might want several colors, if you've got them -- might as well make this pretty!
- Rule: attach the largest square you can: first left, then down, and then continue in a counter-clockwise fashion.
- As you add each square you create a new rectangle. Compute the ratio of side lengths (larger over smaller).
- Do it again, do it again, do it again! (You could do it forever -- but we run out of paper.)
- What do you notice about the dimensions of the rectangle? It's the
ratio of those dimensions that interests us most -- the ratio
of dimensions (larger to smaller) dictates the shape of the
rectangle. Two rectangles that have the same ratio have the
same shape.
1x1 1/1= 2x1 2/1= 3x2 3/2= 5x3 5/3= 8x5 8/5= 13x8 13/8= 21x13 21/13= 34x21 34/21= - The thing we are approaching is the so-called golden rectangle,
whose side-lengths are in the ratio called "the golden
ratio". But we will derive the golden rectangle in a different
way -- the way that the Greeks did it! When we're done, we'll
have also defined the golden mean, aka the golden ratio.
- Nature loves Fibonacci numbers. Many items in nature spiral, and,
if you see spirals, look for Fibonacci numbers:
- Begin with a rectangle.
- Remove the largest square possible from the rectangle, to leave a rectangle.
- If the rectangle that results has exactly the same shape as the original
rectangle, then that rectangle is golden:
However if we look back at the Fibonacci spiral sequence of rectangles as they're growing, we see that they're tending toward a "golden rectangle".
-
If you did your reading (and of course you did!), you know that the
ratios of successive Fibonacci numbers tend toward a certain number,
which is called the "golden mean" or "golden ratio":
\[
\varphi=\frac{1+\sqrt{5}}{2} (\approx 1.618033988749895)
\]
Let's show that this golden ratio is, in fact, the side-length ratio of the golden rectangle described above. And our secret weapon will be your old friend, that old favorite, the quadratic formula!
While we might think about the Fibonacci spirals as being created by attaching squares, the golden rectangle is created by removing squares. We just do things backwards....
We can build beautiful rectangles by pasting squares together, or we can define beautiful rectangles by taking them away....
- Now what can we do with these ideas? Here is a somewhat silly
example -- A Fibonacci spiral fractal comic I made recently, which I
have entitled "Flirting with Death Spiral". Infinite fun!

(sidelengths: 466x288, with ratio 1.6180555555555556!)
You'll be making these, too, soon, using your own photos. Let's do one in class now (if we're lucky this will work!)
- By the way, Salvador Dali's image is sized 334x208: side ratio, 1.6057692307692308
- Euler paths and Euler circuits
- Remember I told you about those dancers, Fred Astair and Ginger Rogers?
Here's a video clip of Fred Astaire and Ginger Rogers. They say Fred Astaire was pretty good (well, "the best dancer ever"); but Ginger Rogers did everything Fred did, only backwards (and in heels...).
That's like this golden rectangle process, and like Egyptian division: backwards and in heels.
- Fibonacci
Spiral Fractal maker.
- How to win at Nim
- Unit Fraction Table
- How Egyptians wrote fractions.
- Problem 81: converting between different measures with fractions
- Egyptian fractions (Wikipedia)
- An amazing source for Egyptian Fraction info
- The new Mayan glyphs from Xultun, Guatemala: lots of spectacular calendar calculations, but nothing whatsoever about 2012 AD
- "Ancient Maya Astronomical Tables from Xultun, Guatemala". William A. Saturno, David Stuart, Anthony F. Aveni, Franco Rossi
- Part of the wall from which our Mayan tablet is taken