-
- This session will be captured on Zoom, if I remember to turn it on, and record it.
- Our page of zooms and the play-by-plays.
- It's our final day! A day to talk about finals, and
finality. Maybe infinity; I usually entangle that with eternity:
When we've been there ten thousand years,
Bright shining as the sun,
We've no less days to sing God's praise,
Than when we first begun.Amazing Grace (John Newton: 1725-1807)
\[ \infty + 10000 = \infty \]
This should remind us of the Hilbert Hotel, which, though full, could accommodate another 10000*365 people; we could shift everyone down 10000*365 rooms, and fit in all those days -- and the hotel would still hold everyone, and be full again! These infinities are the same size.
- We discuss your third (and final) review material today:
recent stuff.
Your final (Wednesday, 12:20-2:20) will come in two parts: old stuff and new stuff. So the review material for Monday and Wednesday was to prepare you for the old stuff.
Today we'll (mostly) hit the new. - Remember you may make the Really
Cool Object as a cheat link for the final. Make it out of 4x6 cards
(it must be constructed if you are to use it).
- You have one homework still outstanding: your knotty problem (due today). I will
post a key here, once I've got them all.
- Got my new copy of Science last night.... and it had a couple of icosahedra in it (of course).
In this course we will consider some of the greatest ideas of humankind, ideas comparable in scale and beauty to the works of Shakespeare, Plato, and Michelangelo. These ideas fall within the domain of mathematics. Mathematics is as much an artistic endeavor as it is a scientific one, and, as such, it requires both imagination and creativity. There are three basic goals for this course:
- To reach a better understanding of several rich mathematical ideas. Pascal's triangle; Platonic solids; golden rectangles; knots; Fibonacci numbers, fractals, and nature
- To develop sharper skills for analyzing life issues that transcend mathematics. Graphs and trees; counting with Pascal's triangle; permitting people to lie to get good answers, using probabilities
- To change the way you view the world! Bigger and bigger infinities! Don't say you've got herpes; say you've been afflicted with a bad case of icosahedra; why is zero such a strange idea?
The fourth goal was for you to make a million dollars playing Fibonacci Nim (remember -- don't call it Fibonacci Nim, because that gives away the strategy). The best Amanda did was five bucks.
- Symmetry:
- rotational -- order 1 if no rotational symmetry
- reflection: it must be exactly the same on the two sides, like when you hold an object up to a mirror. Nature loves bilateral symmetry!
- The regular polygons (are very symmetric polygons), full of rotational and reflection symmetries.
- The radiolarians (e.g Amoeboid protozoa Circogonia
icosahedra) exhibit incredible beauty and symmetry:
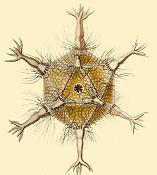
- Symmetry is generally believed to be associated with beauty.
- The Platonic Solids:
- Know their names: Tetrahedron, Hexahedron (or Cube), Octahedron, Dodecahedron, Icosahedron
- Know their characteristics (faces, edges, vertices)
- Know their duals
- Know the Platonic solid graphs -- we project them onto the page (they're planar).
- We created a table that summarized the properties, using
the ideas of duality and Euler's formula to complete
it:
# of Vertices # of Edges # of Faces faces at each vertex sides on each face Tetrahedron 4 6 4 3 3 Cube 8 12 6 3 4 Octahedron 6 12 8 4 3 Dodecahedron 20 30 12 3 5 Icosahedron 12 30 20 5 3
- Fractals (a world within a world (self-similarity)):
-
Simple rules, resulting in fantastic complexity: the trick is
to "Do it again, do it again, ...."
Great fleas have little fleas upon their backs to bite 'em,
And little fleas have lesser fleas, and so ad infinitum.
And the great fleas themselves, in turn, have greater fleas to go on;
While these again have greater still, and greater still, and so on."Siphonaptera" by Augustus De Morgan (published 1872)
The modern version is by Jerry Garcia and Dave Grisman: There Ain't No Bugs On Me:
Well little bugs have littler bugs, upon their backs to bite 'em;
And the littler bugs have still littler bugs, and so ad infinitum. - Nature loves patterns, especially the Fibonacci numbers,
which are created by a fractal process: add the two preceding
numbers; now do it again! Nature probably loves them
because they're fractal, because nature loves fractals.
- The bunny tree is fractal:

Each baby pair starts a sub-tree of the original tree, which is identical to the original tree: there are infinitely many copies of the tree embedded within the tree. Each mature pair starts a sub-tree identical to every other sub-tree started within the tree: infinitely many identical copies, making up the original tree.
"A world within a world." Mathematicians don't need psychodelic drugs, because they have math!:)
- The key is that there is something (e.g. a stick), to which a process is applied and it results in more of the something (e.g. more sticks); and then do it again, do it again, etc. Forever. Ad infinitum. When we do this, we can end up with infinitely long objects within finites spaces, which is a very strange notion....
-
Simple rules, resulting in fantastic complexity: the trick is
to "Do it again, do it again, ...."
- Bands, Links, Knots:
- We studied the bizarre band that keeps on playing: the
mobius band (one-sided, one-edged band), made by giving
a strip of paper a "half-twist" before taping it
together.
- When we snipped it in "two", it did something funny: it stayed in one (the unknot).
- When we snipped a thrice-twisted band in "two", it did something funny: it stayed in one, but it was now a trefoil knot.
- Bands with odd numbers of twists are one-sided, one-edged bands. Cut in "two", they create knots, with numbers of "leaves" corresponding to the number of twists.
- The unknot (no crossings) and the trefoil (three
crossings) are the simplest knots. Then
there's the figure eight knot (the only four crossing
knot); and two five-crossing knots: the cinquefoil (a
torus knot), and the five-twist knot. Those are the
five knots that I expect you to know, and be able to
draw at the drop of a knot.
- Links:
- A zero-twisted band, cut in two, creates the unlink (two "wedding bands"); a twice-twisted band cut in two is called a Hopf link; a four-twisted band cut in two is called Solomon's "knot".
- the Borromean rings are a link that can't be made from a twisted band, involving three rings (any pair of which make an unlink); but they are linked together in such a way that they won't fall apart -- unless any one of them is cut, in which case they all fall apart.
- How do we distinguish knots, or links? Two ways:
- Reidemeister moves (RI, RII, RIII)
- Tri-colorability
- We studied the bizarre band that keeps on playing: the
mobius band (one-sided, one-edged band), made by giving
a strip of paper a "half-twist" before taping it
together.
- Infinity
- Once again the one-to-one correspondence proved
to be the key.
- Power sets -- the set of all subsets of a set --
linked Pascal's triangle back in, and we discovered
that power sets are always bigger than the set from
which they are formed.
This turned out to be true for infinite sets, as well, so that there are an infinite number of bigger and bigger infinities. Mind-blowing!
The natural numbers, even natural numbers, integers, and even the rational numbers (ratios of integers) are all small infinities. They're all the same size, what's called a "countable infinity" ($\aleph_0$).
Interestingly enough, Hebrew letters are used to describe the sizes of infinite sets.
A bigger infinity is the real numbers (including, in particular, all the irrational numbers, like $\pi$, which are as big a set as all the real numbers themselves). Mathematicians speculate that \[ 2^{\aleph_0} = \aleph_1 \] is the size of the real numbers. That would seem to make it the same size as the power set of the natural numbers.
- Once again the one-to-one correspondence proved
to be the key.