Opinionator

Rock Groups

By Steven Strogatz
Steven Strogatz

Steven Strogatz on math, from basic to baffling.

Like anything else, arithmetic has its serious side and its playful side.

The serious side is what we all learned in school: how to work with columns of numbers, adding them, subtracting them, grinding them through the spreadsheet calculations needed for tax returns and year-end reports. This side of arithmetic is important, practical and — for many people — joyless.

The playful side of arithmetic is a lot less familiar, unless you were trained in the ways of advanced mathematics. Yet there’s nothing inherently advanced about it. It’s as natural as a child’s curiosity.

In his book “A Mathematician’s Lament,” Paul Lockhart advocates an educational approach in which numbers are treated more concretely than usual: he asks us to imagine them as groups of rocks. For example, six corresponds to a group of rocks like this:

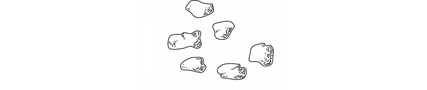
group of rocks

You probably don’t see anything striking here, and that’s right — unless we make further demands on numbers, they all look pretty much the same. Our chance to be creative comes in what we ask of them.

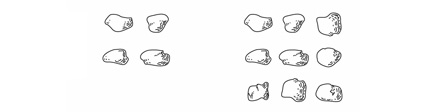
For instance, let’s focus on groups having between 1 and 10 rocks in them, and ask which of these can be rearranged into square patterns. Only two of them can: 4 and 9. And that’s because 4 = 2 × 2 and 9 = 3 × 3; we get these numbers by “squaring” some other number (actually making a square shape).

group of rocks

A less stringent challenge is to identify groups of rocks that can be neatly organized into rectangles with two rows that come out even. That’s possible as long as there are 2, 4, 6, 8 or 10 rocks; the number has to be “even.” All the other numbers from 1 to 10 — the “odd” numbers — always leave an odd bit sticking out.

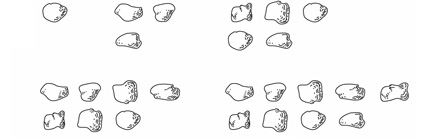
group of rocks

Still, all is not lost for these misfit numbers. If we add two of them together, their protuberances match up and their sum comes out even; Odd + Odd = Even.

group of rocks

Yet when it comes to rectangles, some numbers, like 2, 3, 5 and 7, truly are hopeless. They can’t form any sort of rectangles at all, other than a simple line of rocks. These strangely inflexible numbers are the famous “prime” numbers.

So we see that numbers have quirks of structure that endow them with personalities. But to see the full range of their behavior, we need to go beyond individual numbers and watch what happens when they interact.

For example, instead of adding just two odd numbers together, suppose we add all the consecutive odd numbers, starting from 1:

1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25

The sums above, remarkably, always turn out to be perfect squares. (We saw 4 and 9 in the square patterns discussed earlier, and 16 = 4 × 4, and 25 = 5 × 5.) A quick check shows that this rule keeps working for larger and larger odd numbers; it apparently holds all the way out to infinity. But what possible connection could there be between odd numbers, with their ungainly appendages, and the classically symmetrical numbers that form squares? By arranging our rocks in the right way, we can make this surprising link seem obvious — the hallmark of an elegant proof.

The key is to recognize that odd numbers can make L-shapes, with their protuberances cast off into the corner. And when you stack successive L-shapes together, you get a square!

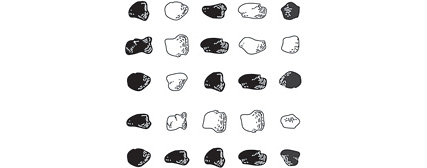
group of rocks

This style of thinking appears in another recent book, though for altogether different literary reasons. In Yoko Ogawa’s charming novel “The Housekeeper and the Professor,” an astute but uneducated young woman with a 10-year-old son is hired to take care of the Professor, an elderly mathematician who has suffered a traumatic brain injury that leaves him with only 80 minutes of short-term memory. Adrift in the present, and alone in his shabby cottage with nothing but his numbers, the Professor tries to connect with the Housekeeper the only way he knows how: by inquiring about her shoe size or birthday and making mathematical small talk about her statistics. The Professor also takes a special liking to the Housekeeper’s son, whom he calls Root, because the flat top of the boy’s head reminds him of the square root symbol, .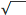

One day the Professor gives Root a little puzzle: Can he find the sum of all the numbers from 1 to 10? After Root carefully adds the numbers and returns with the answer (55), the Professor asks him to find a better way. Can he find the answer without adding the numbers? Root kicks the chair and shouts, “That’s not fair!”

But little by little the Housekeeper gets drawn into the world of numbers, and she secretly starts exploring the puzzle herself. “I’m not sure why I became so absorbed in a child’s math problem with no practical value,” she says. “At first I was conscious of wanting to please the Professor, but gradually that feeling faded and it had become a battle between the problem and me. When I woke in the morning the equation was waiting:

1 + 2 + 3 + … + 9 + 10 = 55

and it followed me all through the day, as though it had burned itself into my retina and could not be ignored.”

There are several ways to solve the Professor’s problem (see how many you can find). The Professor himself gives an argument along the lines we developed above. He interprets the sum from 1 to 10 as a triangle of rocks, with 1 rock in the first row, 2 in the second and so on, up to 10 rocks in the 10th row:

group of rocks

By its very appearance this picture gives a clear sense of negative space. It seems only half complete. And that suggests a creative leap. If you copy the triangle, flip it upside down and add it as the missing half to what’s already there, you get something much simpler: a rectangle with 10 rows of 11 rocks each, for a total of 110.

group of rocks

Since the original triangle is half of this rectangle, the desired sum must be half of 110, or 55.

Looking at numbers as groups of rocks may seem unusual, but actually it’s as old as math itself. The word “calculate” reflects that legacy — it comes from the Latin word “calculus,” meaning a pebble used for counting. To enjoy working with numbers you don’t have to be Einstein (German for “one stone”), but it might help to have rocks in your head.

NOTES:

As I hope I’ve made clear, this piece owes much to two books — one a polemic, the other a novel, both of them brilliant.

The rock metaphor and many of the other ideas and examples above have been borrowed from: Paul Lockhart, “A Mathematician’s Lament: How School Cheats Us Out of Our Most Fascinating and Imaginative Art Form” (Bellevue Literary Press, 2009).

The final example is from: Yoko Ogawa, “The Housekeeper and the Professor” (Picador, 2009).

For young readers who like exploring numbers and the patterns they make, see:

Hans Magnus Enzensberger, “The Number Devil: A Mathematical Adventure” (Holt Paperbacks, 2000).

For elegant but more advanced examples of visualization in mathematics, see:

Roger B. Nelsen, “Proofs without Words: Exercises in Visual Thinking” (Mathematical Association of America, 1997).

Thanks to Carole Schiffman and Tim Novikoff for their comments and suggestions, and to Margaret Nelson for preparing the illustrations.

Response to Comments:

Thanks to the many readers who posted such appreciative comments about the vision for this series.

Regarding some frequently asked questions:

The pieces are scheduled to appear each Monday, for a total of 15 in all.

An RSS feed for the series is available here.

Finally, a correction: in last week’s column I referred to 6 + 6 as an equation, but I should have called it an expression.

Sorry about that, and thank you to the readers who spotted this error.

Editors’ note: The name Hans Magnus Enzensberger was misspelled in the Notes section of an earlier version of this column; it has been corrected.

Need to print this column? Here is a print-friendly PDF version, with images.