These are often depicted as circles, connected by segments, e.g.
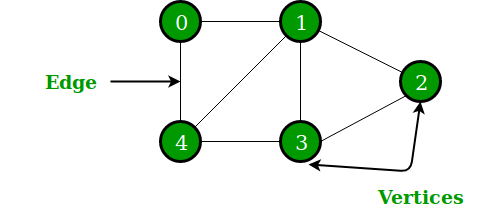
- vertex: a point or node in a graph
- edge (or arc): a connection made between two vertices in a graph
"In the above Graph, the set of vertices V = {0,1,2,3,4} and the set of edges E = {01, 12, 23, 34, 04, 14, 13}." (Thanks to GeeksForGeeks for the image I'm using and this description.)
So in the graph above, vertices 0 and 1 are adjacent (for example), connected by edge 01.
In the graph above, the degree of vertex 4 is three.
In the graph above, no vertex is isolated. But you can imagine that in a graph representing Facebook relationships between friends, for example, some friend may be left out of the group...:(
In the graph above, every vertex is reachable from every other.
If the black segment indicating the vertices in the graph above were actually an edge, then there would be parallel edges connecting vertices 2 and 3.
There are no loops in the graph above.
There is a path from vertex 0 to vertex 2, for example. In fact, there are several! (Can you find at least four different ones, that don't reuse any vertices? A mathematician then asks "Exactly how many such paths are there?")
Are there two paths of length three from vertex 0 to vertex 2?
You can see that there are lots of different cycles in the graph above.
The graph above is not directed. A road map, showing roads between intersections, might use directed edges -- because some roads are one-way: they leave one intersection to go to another, but not vice versa.
The graph above is labeled.
The graph above does not have weighted edges.
The graph above does is not weighted.
The graph above is simple.
The graph above is not complete. For example, there is not edge joining vertex 0 to vertex 2 (so they are not adjacent).
The graph above is not connected.
A face is ultimately two-dimensional, or should be thought of that way.
Would you be surprised to know that a tetrahedron has four faces?