- If you need to Zoom to class, here's the
link.
- Your second exam is this Wednesday. Let's get ready!
- A reminder about some IMath assignments, and the exam:
- You have three IMath assignments -- one each for
the quotient rule, trig rules, and the chain rule. These were
due at the time of the exam. I'm going to delay the chain rule
one (more on that in a bit).
Important Note: you will be expected to show your work for the exam! So, while you might use a calculator, say, to compute a derivative, you will have to be able to show me how you got it using our rules.
- You have three IMath assignments -- one each for
the quotient rule, trig rules, and the chain rule. These were
due at the time of the exam. I'm going to delay the chain rule
one (more on that in a bit).
- Recent whiteboard work:
- Day 15 (last time: the chain rule)
- I'm mostly caught up on grading; I'll be sure to grade your section 2.2 worksheets, starting tonight, and ending around tomorrow midnight, so you'll have those graded before your exam.
- I'm seeing way too many unlabelled graphs. You need to put
numbers on a graph, just for point of reference -- one
can't assume that a tick mark means "1". You don't need
to label every tick mark, but enough to guide the viewer.
- I'm noticing a "Following directions" problem: please, when you're
asked to draw tangent lines, draw tangent lines; when you're
asked to write sentences, write sentences.
Often it's a "two ask" problem: the problem will say "Graph f and the tangent line....", and you, in a hurry, as we all are, just notice the first one. Understandable, but try to avoid that by reading carefully.
- Hint: usually the preview is thoroughly discussed in a section:
it's essentially answered in the discussion, in reading the
section. So if you want to get the "right answers" (or ask
questions about why you're getting something different), you
probably want to read past the preview.
For example, Preview 2.4: the domain of the tangent function is given one "page down" after the preview.
And it's important to read the sections, because I'm relying on you getting certain information from the text that I don't emphasize in class. So, for example, the derivatives of exponential functions with different bases: that is discussed in the text (but in class I stay focused on base $e$, $e^x$ (we'll talk more about this issue when we come to inverse functions, next week).
- There is still some confusion about the limit definition of a
derivative:
Seeing some of this: \[ \tan'(x) \lim_{h \rightarrow 0} = \frac{\tan(x+h)-\tan(x)}{h} \] Seeing some of this: \[ \tan'(x) = \lim_{h \rightarrow 0} \frac{\tan(x+h)-\tan(x)}{h} \] The problem ("traditional problem") is the composition: some people tried \[ \tan'(x) = \lim_{h \rightarrow 0} \frac{\tan(x)+h-\tan(x)}{h} \] Too bad that trick doesn't work (because it would make our jobs so much easier!), but this is not even closely related to
Nothing (certainly not $h$s) magically pops out of compositions....
- Did I mention you need to label your graphs?
- I'm seeing power rules being used on exponential functions.
This is a "traditional error": one we see a lot. Let's figure out what's going on....
For example, $f(x)=2^x$. Some of you tried either $2x$ or $x2^{x-1}$. We can spot the sources of the confusion, so let's talk about those. Here's the right answer, by the way:
\[ f'(x) = \ln(2) 2^x = \ln(2) f(x) \]
Exponentials have this cool property: that their derivatives are proportional to themselves -- it's their superpower.
- Sometimes there is more than one way to look at a function: for example, on your chain rule preview, you had the function \[ f(x)=\left(\tan(x)\right)^2 \] Looks like a composition is most appropriate, but we can also think of $f(x)$ as \[ f(x)=\tan(x)*\tan(x) \] Product rule works!
- We discovered how to compute derivatives of compositions of functions, using the chain rule:
Theorem (the chain rule): If $F(x) = f(g(x))$, and both $f$ and $g$ are differentiable at $x$, then \[ F^\prime(x) = f^\prime(g(x))g^\prime(x) \]
- I personally think about the chain rule this way:
"f prime of stuff times the derivative of the stuff"; or where $f$ is the "outside" function (so $g$ is the "stuff"):"f prime of stuff times stuff prime.",
\[ F^\prime(x) = f^\prime(stuff)stuff^\prime \]
- Here are a couple of relatively easy examples:
- $F(x)=\sin{(x^2)}$
- $F(x)=e^{1 + \sin(x)}$
- A sample problem involving compositions: model the seasonal variation in Keeling's CO2 data:
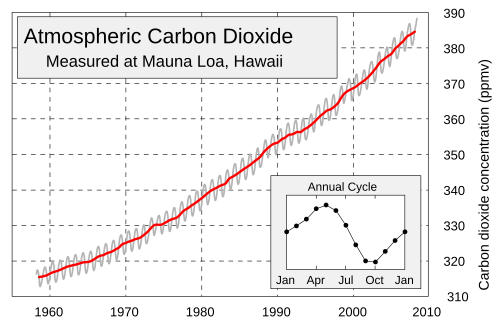
- Keeling data with models:
If time were measured in years from January, would
$V(t)=A\sin(2\pi{t})$ be a good model? What would be a good choice for the parameter $A$?
- Section 1.6: the second (and higher) derivatives
- Section 1.8: the tangent line approximation
- Section 2.1: Elementary derivative rules (sums, differences, powers, exponentials, constant multiples)
- Section 2.2: Derivatives of sines and cosines
- Section 2.3: Product and Quotient rules
- Section 2.4: Derivatives of other trig functions
- Section 2.5: The Chain rule
- The limit definition of the derivative
- The limit definition used to prove one simple rule
- The calculation of some derivatives
- A linearization problem
- Some problems to test general comprehension
- A graphical problem, to make sure that you understand the relationship between a function and its derivative(s) -- e.g. slope and inflection/concavity
We'll approach this topic via some examples:
- Consider the relationship between x and y given by
$y = \frac{1}{x}$ We know how to differentiate y with respect to x, using the power rule.
But there's another way to think about this relationship, and that's
$x y =1$ This gives no priority to either variable. We can still differentiate to find y'(x), however, using the product rule and something called "implicit differentiation". We consider $y$ and unknown (implicitly defined) function of $x$, treating it as $y(x)$; then, since both sides of the equation
$x y(x) =1$ are equal, the derivatives of both sides must be equal. We differentiate both sides, and equate them (using the product rule on the left). From this we obtain the correct derivative, as well.
The solution curves are hyperbolas (one of the conic sections).
- Another example is the folium of Descartes, which is the graph
(solution) of the implicit equation
but\[
x^3 + y^3 = 6xy
\]
Here the equation is perfectly symmetric in $x$ and $y$: it's not at all clear
which variable is dependent, and which independent. By the way, this
symmetry in $x$ and $y$ means that the
solution curve must be symmetric about the line $\displaystyle y=x$:
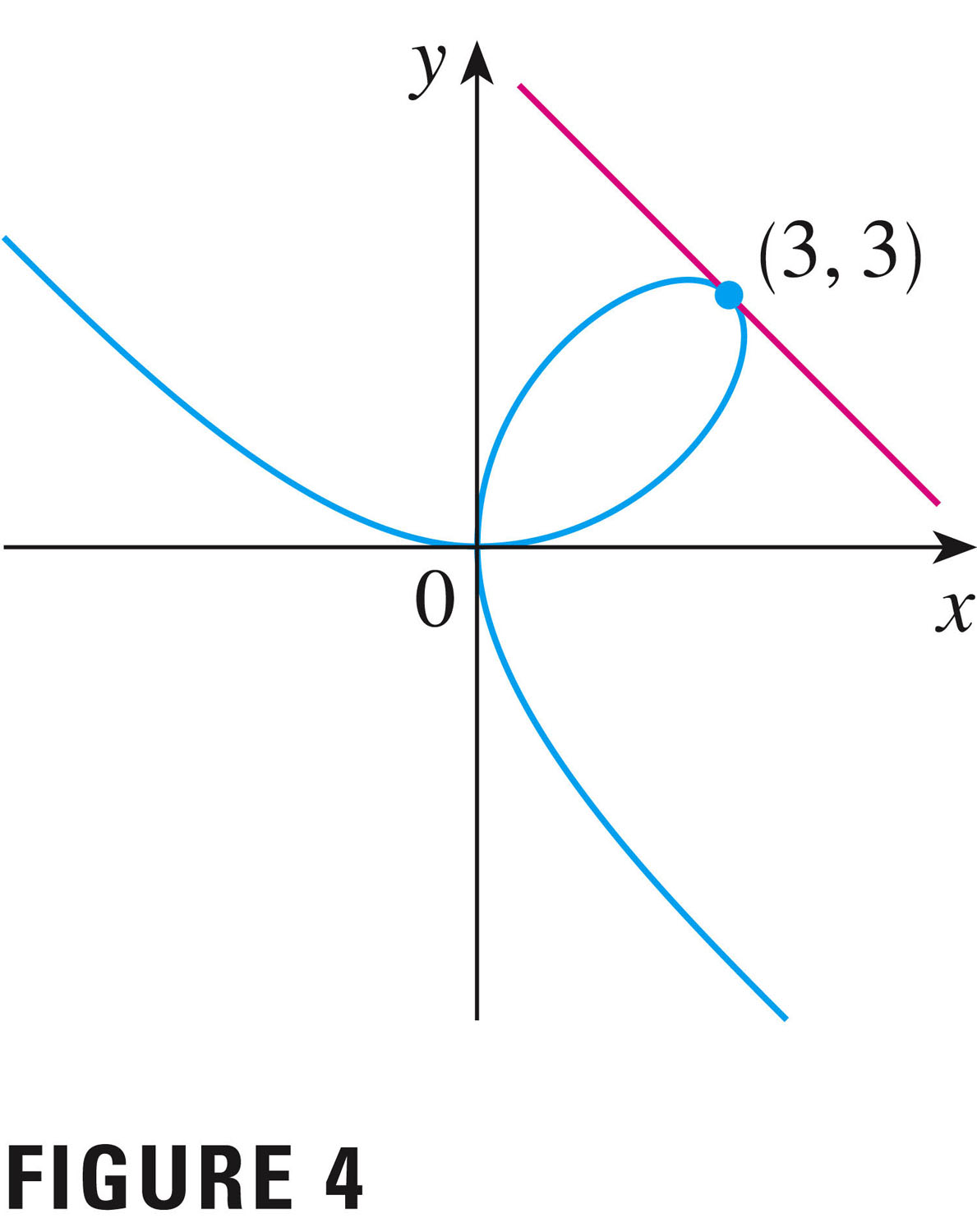
Even though the graph is not the graph of a function (either $y(x)$ or $x(y)$), we can still find tangent lines, etc., using ordinary derivatives. It is the case, however, that a single point in the plane can be represented by several different tangent lines (e.g. the point (0,0)).
- Here's a more complicated relationship between x and y given by
$x^2+y^2=(2x^2+2y^2-x)^2$ 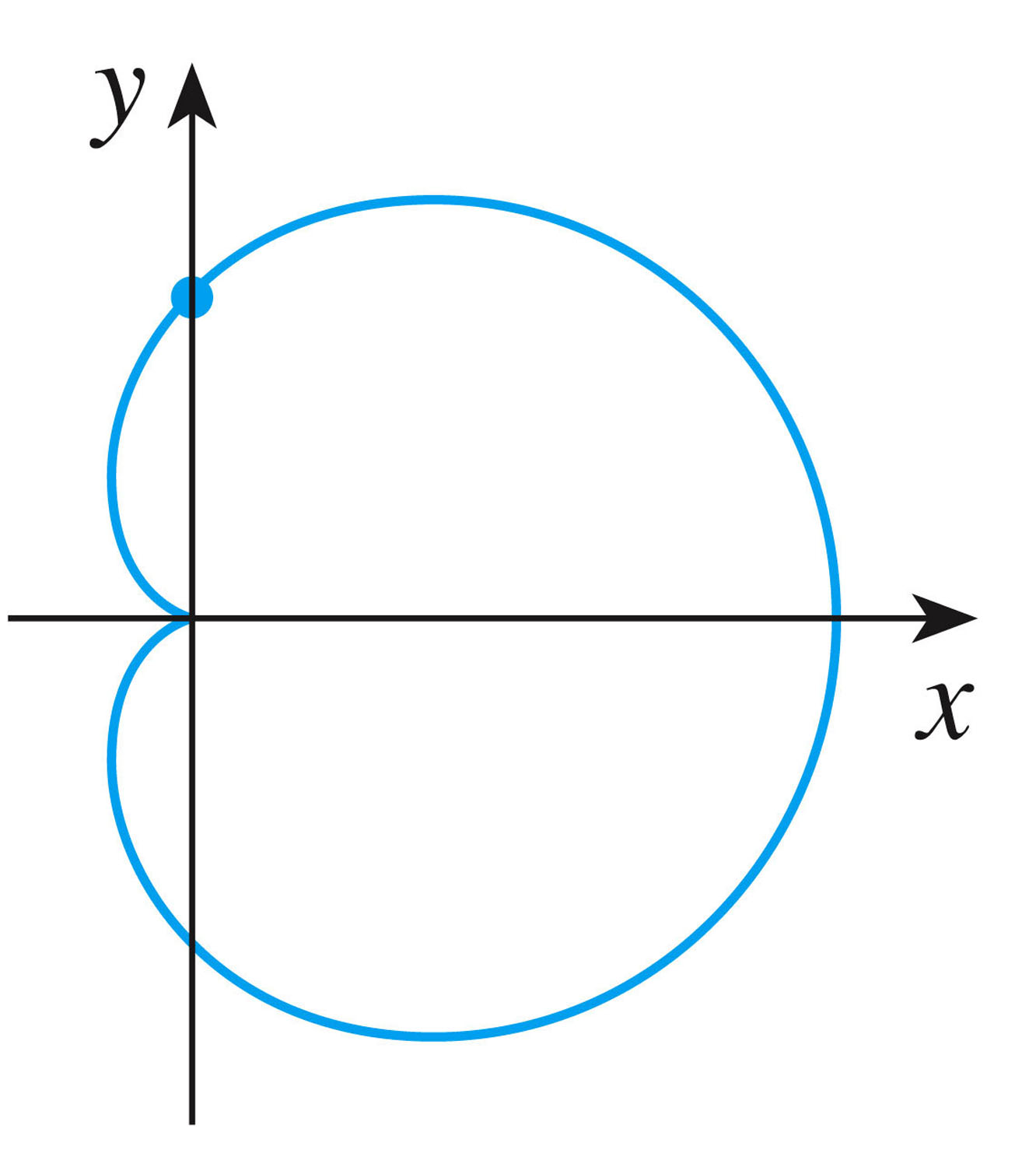
Because the equation is symmetric in $y$ (even in $y$), we expect the curve to be a reflection about the $x$-axis (as it is).