Day 2r, MAT115

• You will have a quiz today over our readings of "From Fish to Infinity" (and the accompanying video), and the portion of the comic book covering sieving primes.

  The prime factorization will be the subject of next week's quiz.

• You have a reading assignment for next time, and some sample prime factorizations to do (use trees...).

• Remember: no class on Monday!

• We reviewed our primes (definitions) and prime factorization (examples), and noted that, to check a number for primeness, you need only consider the primes up to its square root.
• We reviewed some of the interesting features of the primes which we can see in the sieve of Eratosthenes, such as twin primes, the only even prime, etc.
• Then we moved on to the number "six": how Humphrey used the fact that it was composite to try to communicate the order to Ingrid, but when that failed, Ernie suggested that he might use "counting" to deliver the order.
• That led to some new definitions for things like one-to-one correspondence, graphs, and, in particular, complete graphs.

  Let's review those definitions:

  • Definition: a one-to-one correspondence is an association between two sets, so that each member of one set has a unique partner in the other set (and vice versa).
  • Definition: a graph is a collection of points ("vertices") as well as a collection of arcs ("edges" -- each of which joins two points).

    An edge can even join a vertex to itself, which is called a loop in a graph.

    

  • Definition: If every vertex in a graph is connected to every other (different) vertex by a single arc, we call it a complete graph.
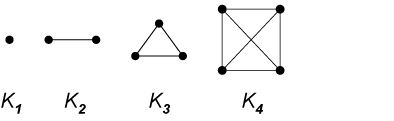
  • Trees are examples of graphs. Our trees so far have points which are numbers, and the arcs represent that one number is a factor of another number: Definition: A tree is a graph with two properties that graphs don't possess in general:
    • a tree has a special point (vertex), called "root";
    • a tree has no "circuits" -- no paths that lead off from a point and then arrive back eventually, as in the tetrahedron.
    That means that there's a unique path between any two vertices (which is not true for tetrahedron, because there are circuits in that graph).

• Then we tried to figure out a pattern to the number of connections (arcs, or edges) the complete graphs have as the number of points grow.

  Each time we add a new point (vertex), we have to connect it to the other points (vertices): so how do the number of connections grow with the number of points? We want a formula:

  $arcs(nvertices)=....$

  To get the answer, we start with a table, and try to figure out the pattern (remember, mathematicians are pattern lovers!).

  $K_n$ $arcs(K_n)$ 1 0 2 1 3 3 4 6 5 10

  Let's revisit that, and start again with $K_5$:

  

  Let's use symmetry to solve this (symmetry is one of the topics that we're going to study down the road...).

  This problem is related to another story, about a little boy who became the greatest mathematician of all time.... Carl Friedrich Gauss ("the Prince of Mathematicians").

  The story is told in a different way in one of your readings (The Loneliest Numbers).

A strange side-note:

The French defined the meter as one ten-millionth of the distance between the equator and the north pole on a great circle passing through Paris (makes perfect sense to me....:). So the government put official "meter sticks" around the city, so that anyone could check their measures (e.g. a piece of cloth) with this "official" meter.

In Paris there is still one of the "sticks" (it's marble!) "standing" (well, actually it's along a wall at a bus stop in Paris):

So should we create marble statues of six fingers being held up, with a sign saying "six"?

Perfect matching: we will indicate the number six with something that yells "Six" to everyone. You can bring up "six" candy bars, to see if you really have six -- by matching them to fingers of marble....

But then we'd need a statue with seven fingers, and five fingers, and 37 fingers, and .....

Or we could just count...:)

1. Do you have a favorite number? If so, do you know why?
2. One is the loneliest number, but
3. Two can be as bad as one; it's the loneliest number since the number one.
4. I can prove that all counting numbers are interesting, using order! Let me start with a story, however, about the number 1729¹...

   G. H. Hardy	Srinivasa Ramanujan

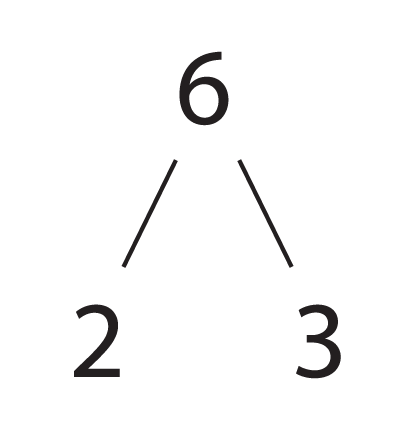
Other numbers seem very gregarious; they play well with other numbers (e.g. 6, which seems particular friendly with 2 and 3; or 12, which has lots of friends: 2,3,4,6!).

But how can we understand "6" without understanding "5" as well? (and thus 4, 3, 2, 1,...0?) We'll discover that 0 was pretty hard to understand from early on!