Exponential functions can be used to understand many natural phenomena, including bacterial growth and radioactive decay. Before we get into these applications we will cover some of the basic mathematics you need to know to use these functions.

What is an exponential function?

Definition - An exponential function, f (x), with base a is defined by:

f (x) = a ^x

where a > 0, and a ≠ 1.

 

The domain (potential values of x) of an exponential function is all real numbers or (− ∞, ∞), while the range (potential values of y) is all positive real numbers or ( 0, ∞).

Some examples of exponential functions are:

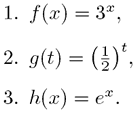
Notice that the base of the exponential function, a > 0, may be greater than or less than one. This distinction will be important when inspecting the graphs of the exponential functions.

We have eliminated the case a = 1, since 1 ^x = 1, for all x. We will see in the next section that a = 1 is the boundary between exponential growth and exponential decay.

Also note in sample function 3 we use the irrational number e (≈ 2.718) as a base. Base e exponential functions are sometimes called natural exponential functions and they commonly appear in the sciences. We will encounter base e throughout our discussion of exponential and logarithmic functions.

A common mistake you should avoid

Exponential functions may look similar to functions like, y = x ³. Of course, upon closer inspection, they are quite different. Notice the position of the variable x. For exponential functions (e.g. y = 3 ^x), the variable x is in the superscript position (exponent), and the constant 3 is the base. On the other hand, for the case of x ³, the constant 3 is in the superscript position over the variable x.

*****

In the next section we will review the rules governing the use of exponentials.